7 Gibbs Distribution
So far, we have considered closed systems and derived and studied the Boltzmann distribution. Now our systems are open and the particle number might change. The Boltzmann distribution is therefore not anymore sufficient to describe the probability to find a system with an energy \(E_\mathrm{s}\) and a particle number \(N_\mathrm{s}\) in contact with a reservoir. To derive a distribution for this new situation, we can use one of the ways, which also allowed the derivation of the Boltzmann distribution. This route is, again, considering the ratio of the proababilities of two arbitrary states of the system (index s) which is equal to the ratio of the numbers of possible states of the reservoir (index \(r\)):
\[\begin{equation} \frac{p(E_\mathrm{s}^{(1)},N_\mathrm{s}^{(1)})}{p(E_\mathrm{s}^{(2)},N_\mathrm{s}^{(2)})}=\frac{W_\mathrm{r}(E_\mathrm{tot}-E_\mathrm{s}^{(1)},N_\mathrm{tot}^{(1)})}{W_\mathrm{r}(E_\mathrm{tot}-E_\mathrm{s}^{(2)},N_\mathrm{tot}^{(2)})} \end{equation}\]
Hereby, the \(E_\mathrm{s}^{(i)}, N_\mathrm{s}^{(i)}\) denote the energy and the number of particles in the system in the \(i\)th state. \(W_\mathrm{r}\) indicates the number of available states to the reservoir, when the system is in a specific energy state with a specific number of particles. Similar to the derivation of the Boltzmann distribution, we can now assert that the total number of available states of the system and the reservoir is given by
\[\begin{equation} W_\mathrm{tot}(E_\mathrm{tot}-E_\mathrm{s}^{(1)},N_\mathrm{tot}-N_\mathrm{s}^{(1)})=1\times W_\mathrm{r}(E_\mathrm{tot}-E_\mathrm{s}^{(1)},N_\mathrm{tot}-N_\mathrm{s}^{(1)}). \end{equation}\]
Note that the system is in exactly one state in this case. Utilizing again that \(S=k_\mathrm{B} \ln(W)\) or \(W=\exp(S/k_\mathrm{B})\), we find
\[\begin{equation} \frac{W_\mathrm{r}^{(1)}}{W_\mathrm{r}^{(2)}}=\frac{\exp(S_\mathrm{r}^{(1)}/k_\mathrm{B})}{\exp(S_\mathrm{r}^{(2)}/k_\mathrm{B})}. \end{equation}\]
Once more, we can use a first order expansion to get
\[\begin{equation} S_\mathrm{r}(E_\mathrm{tot}-E_\mathrm{s},N_\mathrm{tot}-N_\mathrm{s})\approx S_\mathrm{r}(E_\mathrm{tot},N_\mathrm{tot})-\frac{\partial S_\mathrm{r}}{\partial E}E_\mathrm{s}-\frac{\partial S_\mathrm{r}}{\partial N}E_{N_\mathrm{s}}. \end{equation}\]
The partial derivatives can be converted with the help of the known thermodynamic relations
\[\begin{equation} \frac{\partial S_\mathrm{r}}{\partial E}\bigg|_{V,N} =\frac{1}{T} \end{equation}\]
and
\[\begin{equation} \frac{\partial S_\mathrm{r}}{\partial N}\bigg|_{V,E}=-\frac{\mu}{T} \end{equation}\]
which finally yields the Gibbs distribution:
Gibbs distribution
\[\begin{equation} p(E_\mathrm{s}^{(1)},N_\mathrm{s}^{(1)})=\frac{1}{Z}\exp\left ( -\frac{E_\mathrm{s}^{(1)}-\mu N_\mathrm{s}^{(1)} }{k_\mathrm{B} T} \right ) \end{equation}\]
with the grand partition function
\[\begin{equation} Z=\sum_{i}\exp \left ( -\frac{E_\mathrm{s}^{(i)}-\mu N_\mathrm{s}^{(i)}}{k_\mathrm{B} T}\right ). \end{equation}\]
Ligand Binding
As an example, we have a look at the binding of a ligand (green) to a receptor, which is indicated in the figure below.
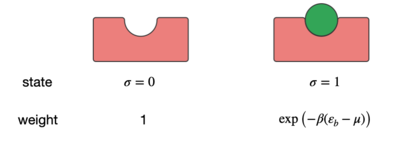
The binding is reported by the variable \(\sigma\), which can be either 0 or 1. The binding energy is therefore
\[ E=\sigma \varepsilon_\mathrm{b} \]
with \(\varepsilon_\mathrm{b}<0\), since the ligand wants to bind. The grand partition function
\[ Z=\sum_\mathrm{states}\exp\left ( -\beta (E_\mathrm{state}- \mu N_\mathrm{state}) \right ), \]
in which the chemical potential \(\mu\) reflects the contact with the particle reservoir and \(\beta=(k_\mathrm{B}T)^{-1}\), can therefore be written as:
\[ Z=\sum_{\sigma=0}^{1}\exp\left ( -\beta (\varepsilon_\mathrm{b} \sigma- \mu \sigma) \right )=1+\exp(-\beta (\varepsilon_\mathrm{b} -\mu )). \]
From that we can calculate the mean number of bounded ligands to be
\[ \langle N \rangle =\frac{\exp(-\beta (\varepsilon_\mathrm{b} -\mu ))}{1+\exp(-\beta (\varepsilon_\mathrm{b} -\mu ))}. \]
Using
\[ \mu = \mu_0 + k_\mathrm{B} T \ln \left ( \frac{c}{c_0}\right ) \]
we can finally write
\[ \langle N \rangle =\frac{c/c_0 \exp(-\beta \Delta \varepsilon_\mathrm{b})}{1+\frac{c}{c_0}\exp(-\beta \Delta \varepsilon_\mathrm{b})} \]
with \(\Delta \varepsilon_\mathrm{b}=\varepsilon_\mathrm{b}-\mu_0\), which is the energy freed when taking the ligand from the solution and placing it at the acceptor.