Refraction and Total Internal Reflection

Refraction

Historical Context of Refraction

The understanding of refraction has evolved over centuries, with contributions from various cultures and scientific traditions. This timeline highlights key milestones in the discovery and formalization of refraction, showcasing how our comprehension of this fundamental optical phenomenon has deepened over time:

1. Ancient Greece (3rd century BCE): Euclid noticed that a stick partially submerged in water appears bent. Archimedes studied the refraction of light in water.

2. Ancient Rome (1st century CE): Ptolemy conducted experiments on refraction and compiled tables of refraction angles for different media.

3. Islamic Golden Age (10th-11th centuries): Ibn Sahl (940-1000) discovered the law of refraction, describing it geometrically. Alhazen (965-1040) studied lenses and the human eye, contributing significantly to optics.

4. Middle Ages: Robert Grosseteste (1175-1253) and Roger Bacon (1214-1294) studied refraction and its application to lenses.

5. Renaissance: Thomas Harriot (1560-1621) rediscovered the law of refraction but didn’t publish his findings.

6. 17th Century: Willebrord Snellius (1580-1626) derived the mathematical law of refraction (Snell’s law) around 1621. René Descartes (1596-1650) independently derived and published the law of refraction in 1637. Pierre de Fermat (1607-1665) derived the law of refraction using his principle of least time.

7. 19th Century: Augustin-Jean Fresnel (1788-1827) developed the wave theory of light, explaining refraction in terms of changes in wave speed.

8. 20th Century: The quantum mechanical understanding of light, which emerged in the early 20th century, significantly impacted our view of refraction. Max Planck’s work on black body radiation in 1900 and Albert Einstein’s explanation of the photoelectric effect in 1905 laid the groundwork for the quantum nature of light. This quantum perspective provided a complementary explanation to the wave theory, describing refraction in terms of photons interacting with the atoms in the medium. While this quantum view offers insights into certain aspects of refraction, it’s important to note that both the wave and particle descriptions of light are necessary for a complete understanding of optical phenomena.

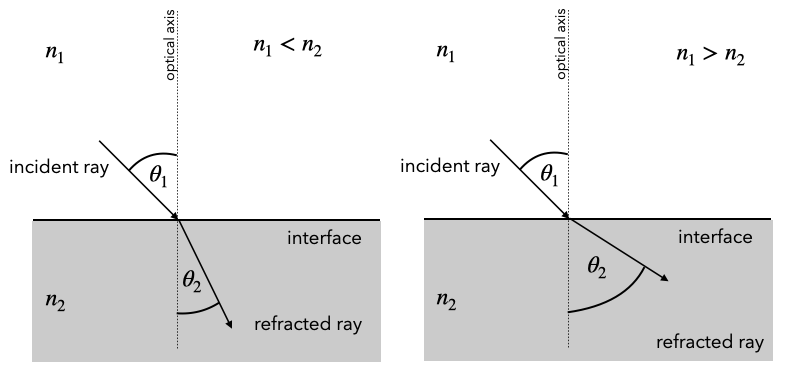
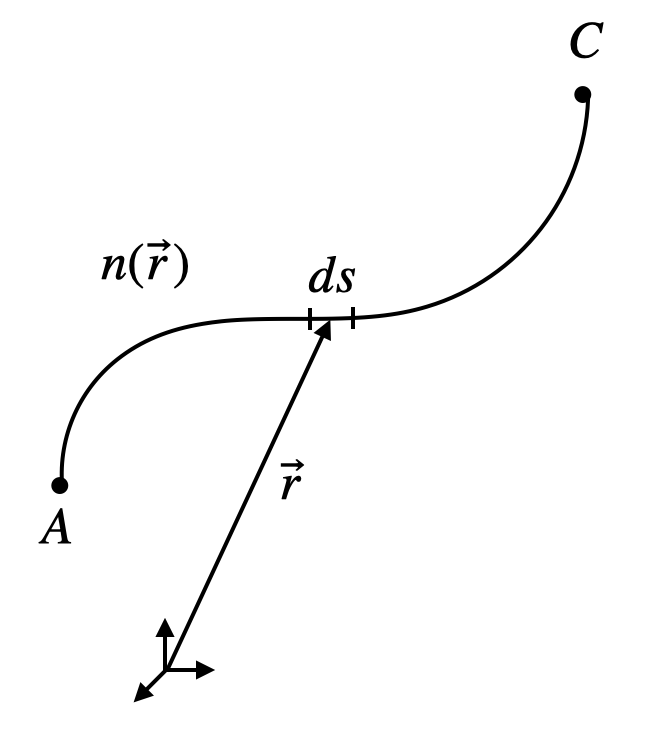
The law of refraction is the second important law of geometrical optics. It relates the refractive index $n_1$ and angle of incidence ${\theta }_1$ on one side of an interface to the refractive index $n_2$ and angle of refraction ${\theta }_2$ on the other side. Both the law of reflection and the law of refraction can be derived from more fundamental principles such as Fermat’s principle of least time and are consistent with the conservation of energy. Their relation to momentum is more complex and involves considering the interaction of light with the medium at an atomic level. These laws provide a mathematical framework for predicting how light behaves when it encounters interfaces between different media, forming the basis for understanding a wide range of optical phenomena and the design of optical devices.

Refractive Index

The refractive index $n$ is a material constant representing the factor by which the speed of light is reduced in the medium compared to its speed in vacuum. For most natural materials and visible light, the refractive index is $n\ge 1$, as light typically travels slower in media than in vacuum. However, in certain special cases—such as for X-rays in some materials or in engineered metamaterials—the refractive index can be less than 1 or even negative. Understanding these exotic cases requires a deeper exploration of the electromagnetic properties of materials and the origin of the refractive index, which we will address later.

Snells Law

Law of Refraction (Snell’s Law)

The law of refraction (Snell’s law) is given for the above sketch by the equation:

$$n_1\sin ({\theta }_1)=n_2\sin ({\theta }_2)$$

You can explore the law of refraction using the interactive visualization below. The visualization shows a light ray incident on an interface between two media with different refractive indices. You can adjust the angle of incidence and the refractive index of the first medium to see how the angle of refraction changes according to Snell’s law.

Incident Angle: 45°

Refractive Index n₁: 1.0

Refractive Index n₂: 1.5

Snell’s law leads to some general patterns in the behavior of light rays at interfaces, which are worth remembering. Consider these two cases:

1. When light moves from a medium with lower refractive index to one with higher refractive index ($n_1<n_2$):
   • The refracted ray bends towards the normal (optical axis)
   • The angle of refraction is smaller than the angle of incidence (${\theta }_2<{\theta }_1$)
2. When light moves from a medium with higher refractive index to one with lower refractive index ($n_1>n_2$):
   • The refracted ray bends away from the normal (optical axis)
   • The angle of refraction is larger than the angle of incidence (${\theta }_2>{\theta }_1$)

Figure 1 illustrates these principles with three plots showing how the refracted angle changes with the incident angle for two common interface scenarios: glass-to-air and air-to-glass. These plots clearly demonstrate the different behaviors described above.

def snell(n1, n2, theta1):
    sin_theta2 = n1 * np.sin(theta1) / n2
    theta2 = np.arcsin(np.clip(sin_theta2, -1, 1))
    theta2[sin_theta2 > 1] = np.nan
    return theta2

fig, ax = plt.subplots(figsize=(4, 4))

theta1 = np.linspace(0, np.pi/2, 1000)

theta2_1_to_1_5 = snell(1.0, 1.5, theta1)
theta2_1_5_to_1 = snell(1.5, 1.0, theta1)
theta2_1_to_1 = snell(1.0, 1.0, theta1)

ax.plot(np.degrees(theta1), np.degrees(theta2_1_to_1_5), color='blue')
ax.plot(np.degrees(theta1), np.degrees(theta2_1_5_to_1), color='red')
ax.plot(np.degrees(theta1), np.degrees(theta2_1_to_1), color='green', linestyle='--')

ax.set_xlabel(r'$\theta_1$ [°]')
ax.set_ylabel(r'$\theta_2$ [°]')
ax.set_xlim(0, 90)
ax.set_ylim(0, 90)

ax.plot([0, 90], [0, 90], color='gray', linestyle=':', label='y=x')

ax.annotate(r'$\frac{n_2}{n_1}=1.5$', xy=(60, 35), xytext=(50, 20),
            arrowprops=dict(arrowstyle='->'), color='blue')
ax.annotate(r'$\frac{n_1}{n_2}=1.5$', xy=(30, 50), xytext=(10, 70),
            arrowprops=dict(arrowstyle='->'), color='red')
ax.annotate(r'$\frac{n_2}{n_1}=1$', xy=(45, 45), xytext=(65, 50),
            arrowprops=dict(arrowstyle='->'), color='green')

plt.tight_layout()
plt.show()

Figure 1— Snell’s law for different combinations of refractive indices. The plots show the relationship between incident angle (${\theta }_1$) and refracted angle (${\theta }_2$) for three scenarios: (a) light passing from air to glass, (b) light passing from glass to air, and (c) a comparison of both cases. Note how the curves differ when light moves into a medium with higher refractive index versus a lower refractive index.

Total Internal Reflection

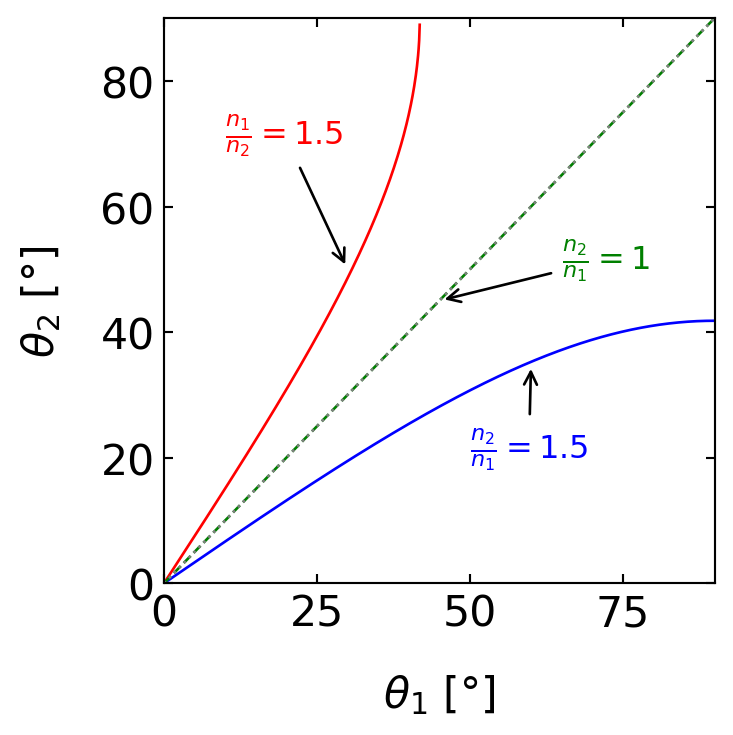
The above diagram reveals a special case occurring when $n_1>n_2$. Under these conditions, we can increase the incident angle ${\theta }_1$ until the outgoing angle reaches ${\theta }_2=\frac{\pi }{2}$. At this point, the refracted ray would be traveling along the interface between the two media. For any incident angle ${\theta }_1$ larger than this critical angle, there is no refracted ray at all; instead, we observe only a reflected ray. This phenomenon, known as total internal reflection, occurs despite the fact that the material with refractive index $n_2$ is completely transparent.

Let’s formalize this concept mathematically. Using Snell’s law and setting ${\theta }_2=\frac{\pi }{2}$, we obtain the equation for the critical angle ${\theta }_c$:

$${\theta }_1={\theta }_c={\sin }^{-1}\left(\frac{n_2}{n_1}\right)$$

Note that the ${\sin }^{-1}()$ function requires an argument $\le 1$, which is why this phenomenon only occurs when $n_2<n_1$.

It’s important to understand that during total internal reflection, all of the light energy is reflected back into the first medium, hence the term ‘total’. However, electromagnetic optics reveals an interesting subtlety: an evanescent wave penetrates a short distance into the second medium, though it doesn’t propagate energy across the boundary.

When the incident angle exceeds the critical angle, Snell’s law as we’ve written it no longer applies. Instead, we observe perfect reflection, where the angle of reflection equals the angle of incidence, just as in regular reflection from a mirror. This reflection occurs without any loss of energy to the second medium, making it an extremely efficient process.

Total Internal Reflection

Total internal reflection occurs when light is passing from higher refractive index to lower refractive index materials for incidence angle larger than a critical angle

$${\theta }_c={\sin }^{-1}\left(\frac{n_2}{n_1}\right)$$

We can demonstrate total internal reflection very easily with a water basin, for example, where we couple in light from a laser from the side.

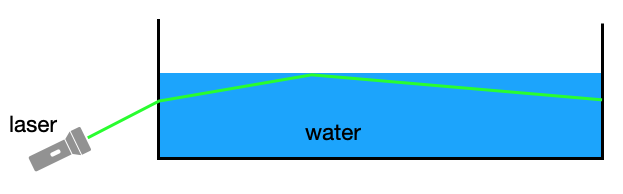
But you could try that yourself also in the bath tub diving below the water surface.

Total internal reflection has numerous practical applications:

1. Fiber optic communications: Light signals can travel long distances with minimal loss through optical fibers.
2. Optical instruments: Prisms in binoculars and telescopes use total internal reflection to manipulate light paths.
3. Gemstones: The sparkle of diamonds is enhanced by total internal reflection trapping light within the stone.
4. Medical endoscopes: Total internal reflection helps guide light through flexible tubes for internal imaging.

Optical Fibers and Total Internal Reflection

Total internal reflection plays a crucial role in modern telecommunications, particularly in optical fibers, which are also part of many experimental setups. These fibers are essentially ultra-thin glass wires, ranging in diameter from a few micrometers to several hundred micrometers, designed to transport light over long distances with minimal loss.

The structure of an optical fiber is key to its function:

1. Core: A central glass core with a refractive index $n_1$
2. Cladding: A surrounding layer with a slightly lower refractive index $n_2$

This difference in refractive indices is what allows total internal reflection to occur within the fiber.

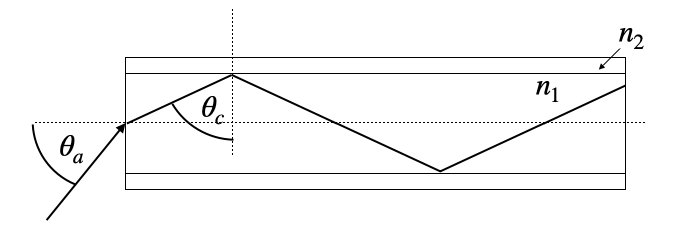
For light to propagate effectively through the fiber, it must enter at an angle that ensures total internal reflection at the core-cladding interface. This leads to the concept of the acceptance angle, ${\theta }_a$, which is the maximum angle at which light can enter the fiber and still undergo total internal reflection.

To characterize this acceptance angle, optical engineers use a parameter called the Numerical Aperture (NA).

Numerical Aperture

The Numerical Aperture of a fiber is defined as the sine of the maximum acceptance angle:

$$NA=\sin ({\theta }_a)=\sqrt{n_1^2-n_2^2}$$

This equation relates the NA directly to the refractive indices of the core and cladding. The derivation of this formula involves applying Snell’s law at the air-fiber interface and at the core-cladding interface, then using the condition for total internal reflection.

In practice, typical values for the refractive indices might be $n_1=1.475$ for the core and $n_2=1.46$ for the cladding. Plugging these into our equation:

$$NA=\sqrt{{1.475}^2-{1.46}^2}\approx 0.2$$

This means that light entering the fiber within a cone of about 11.5° (arcsin(0.2)) from the fiber’s axis will be transmitted through the fiber via total internal reflection.

The NA is an important parameter in fiber optic design:

1. It determines the light-gathering ability of the fiber.
2. It affects the fiber’s bandwidth and its susceptibility to certain types of signal distortion.
3. It influences how easily the fiber can be coupled to light sources and other fibers.

Optical fibers come in various types, each optimized for different applications. Some fibers are designed to transmit light over long distances with minimal loss, while others are engineered for specific wavelengths or to guide light in unusual ways. The figure below shows a few examples of optical fiber types.

Figure 2— Rendering of different optical fibers types (from left to right): Hollow core optical fiber, hollow core bragg fiber, photonic crystal fiber, conventional fiber

Fermat’s Principle for Inhomogeneous Media

While before we have considered Fermat’s principle for the special case of refraction and light propagation in a homogeneous medium, we can define a more general version of it correponding to the following situation also involving an inhomogeneous refractive index $n(\overrightarrow{r})$.

Figure 3— Sketch for a general description of Fermat’s principle

For this general scenario of light traveling along a path, we can define an optical path length (OPL) as

$$\text{OPL}=\underset{A}{\overset{C}{\int }}n(\mathbf{r})\mathrm{d}s=0,$$

with a varying refractive index $n(\mathbf{r})$. Fermat’s Principle states that the actual path taken by the light makes the OPL stationary:

$$\delta ({\int }_A^{B}n(\mathbf{r})ds)=0$$

Using the calculus of variations, this leads to the Euler-Lagrange equation for the path of light. In Cartesian coordinates, if the path is parameterized by $\mathbf{r}(s)=(x(s),y(s),z(s))$, the Euler-Lagrange equations become:

$$\frac{d}{ds}\left(n\frac{d\mathbf{r}}{ds}\right)=\mathrm{\nabla }n$$

where $\mathrm{\nabla }n$ is the gradient of the refractive index. This equation describes how the light ray bends in response to changes in the refractive index of the medium.

Fermat’s Principle is a cornerstone of geometrical optics and has applications in designing optical systems, understanding mirages, and analyzing the behavior of light in various media.

Fermat’s Principle and Snells Law

We would like to apply Fermat’s principle to derive Snell’s law, which is a more lengthy calculation. To do this, we consider a light ray traveling from point $A$ in medium 1 (with refractive index $n_1$) to point $C$ in medium 2 (with refractive index $n_2$), crossing the interface at point $B$. Let the coordinates of points $A$, $B$, and $C$ be $(x_A,y_A)$, $(x_B,y_B)$, and $(x_C,y_C)$, respectively. Assume the interface between the two media is at $y=y_B$. The optical path length (OPL) is given by:

$$\delta {\int }_A^{C}n(\overrightarrow{r})ds=0,$$

where $n(\overrightarrow{r})$ is the refractive index at position $\overrightarrow{r}$, and $ds$ is an infinitesimal element of the path.

Consider a light ray traveling from point $A$ in medium 1 (with refractive index $n_1$) to point $C$ in medium 2 (with refractive index $n_2$), crossing the interface at point $B$. Let the coordinates of points $A$, $B$, and $C$ be $(x_A,y_A)$, $(x_B,y_B)$, and $(x_C,y_C)$, respectively. Assume the interface between the two media is at $y=y_B$.

Optical Path Length

The optical path length (OPL) is given by:

$$\text{OPL}=n_1{\int }_A^{B}d{s}_1+n_2{\int }_B^{C}d{s}_2,$$

where $d{s}_1$ and $d{s}_2$ are the infinitesimal path lengths in media 1 and 2, respectively.

Path Lengths

The path lengths $d{s}_1$ and $d{s}_2$ can be expressed in terms of the coordinates:

$$d{s}_1=\sqrt{(d{x}_1{)}^2+(d{y}_1{)}^2},d{s}_2=\sqrt{(d{x}_2{)}^2+(d{y}_2{)}^2}.$$

Since the interface is at $y=y_B$, we have $d{y}_1=y_B-y_A$ and $d{y}_2=y_C-y_B$. The total optical path length is:

$$\text{OPL}=n_1\sqrt{(x_B-x_A{)}^2+(y_B-y_A{)}^2}+n_2\sqrt{(x_C-x_B{)}^2+(y_C-y_B{)}^2}.$$

Applying Fermat’s Principle

To find the stationary path, we take the variation of the OPL with respect to $x_B$:

$$\delta \text{OPL}=\delta [n_1\sqrt{(x_B-x_A{)}^2+(y_B-y_A{)}^2}+n_2\sqrt{(x_C-x_B{)}^2+(y_C-y_B{)}^2}]=0.$$

Taking the derivative with respect to $x_B$:

$$\frac{\partial }{\partial x_B}[n_1\sqrt{(x_B-x_A{)}^2+(y_B-y_A{)}^2}+n_2\sqrt{(x_C-x_B{)}^2+(y_C-y_B{)}^2}]=0.$$

Differentiating

Differentiating each term separately:

$$n_1\frac{\partial }{\partial x_B}\sqrt{(x_B-x_A{)}^2+(y_B-y_A{)}^2}+n_2\frac{\partial }{\partial x_B}\sqrt{(x_C-x_B{)}^2+(y_C-y_B{)}^2}=0.$$

Using the chain rule:

$$n_1\frac{x_B-x_A}{\sqrt{(x_B-x_A{)}^2+(y_B-y_A{)}^2}}+n_2\frac{x_B-x_C}{\sqrt{(x_C-x_B{)}^2+(y_C-y_B{)}^2}}=0.$$

Simplifying

Let ${\theta }_1$ be the angle of incidence and ${\theta }_2$ be the angle of refraction. Then:

$$\sin {\theta }_1=\frac{x_B-x_A}{\sqrt{(x_B-x_A{)}^2+(y_B-y_A{)}^2}},\sin {\theta }_2=\frac{x_C-x_B}{\sqrt{(x_C-x_B{)}^2+(y_C-y_B{)}^2}}.$$

Substituting these into the equation:

$$n_1\sin {\theta }_1+n_2\sin {\theta }_2=0.$$

Since $\sin {\theta }_2$ is in the opposite direction, we have:

$$n_1\sin {\theta }_1=n_2\sin {\theta }_2.$$

This is Snell’s law, which describes the relationship between the angles of incidence and refraction when light passes from one medium to another.

Conclusion

By applying Fermat’s principle and taking the variation of the optical path length, we have derived Snell’s law:

$$n_1\sin {\theta }_1=n_2\sin {\theta }_2.$$

This demonstrates how the principle of least time leads to the well-known law of refraction in optics.

Example: Light in a Graded-Index Medium

Consider a medium where the refractive index varies with height $y$ as $n(y)=n_0(1-\frac{{\alpha }^2}{2n_0}{y}^2)$. The path of light in such a medium can be found by using Fermat’s principle in differential form:

$$\frac{d}{ds}(n(\mathbf{\text{r}})\frac{d\mathbf{\text{r}}}{ds})=\mathrm{\nabla }n(\mathbf{\text{r}})$$

Typically, this requires to express the coordinates in terms of a parameter, such as $x(s)$ and $y(s)$, and then solve the differential equation. The solution will give the path of light in the medium. This is difficult and commonly done numerically. In paraxial optics, when the light is propagating roughly in the direction of $z$, the differential element $ds$ can be approximated as $dz$ since then

$$ds=dz\sqrt{1+{\left(\frac{dy}{dz}\right)}^2+{\left(\frac{dx}{dz}\right)}^2}\approx dz$$

which yields

$$\frac{d}{dz}\left(n\frac{dx}{dz}\right)\approx \frac{dn}{dx}$$

and

$$\frac{d}{dz}\left(n\frac{dy}{dz}\right)\approx \frac{dn}{dy}$$

This readily yields the path of light in a homogeneous medium, where $n$ is constant. In this case we have

$$\frac{d^{2}x}{d{z}^2}=\frac{d^{2}y}{d{z}^2}=0$$

which is true for a straight line. In a graded-index medium, the path of light can be found by solving the differential equation

$$\frac{d^{2}y}{d{z}^2}=-{\alpha }^{2}y$$

which is reminiscent of the equation of motion of a harmonic oscillator. The solution is therefore an oscillating function

$$y(z)=y_0\cos (\alpha z)+\frac{{\theta }_0}{\alpha }\sin (\alpha z)$$

where the angle ${\theta }_0$ is the initial angle of the light ray with respect to the $z$ axis. This solution describes the path of light in a graded-index medium.

Fermats’s Principle in Integral and Differential Form

We have described Fermat’t principle in an integral form specifiying the optical path length $S$ as

$$OPL=\int n(\mathbf{\text{r}})ds$$

The path length $ds$ can be given in terms of two coordinates $x_1$ and $x_2$ parametrized by $\lambda$ such that

$$ds=\sqrt{{\dot{x}}_1^2+{\dot{x}}_2^2}d\lambda$$

where ${\dot{x}}_1=\frac{d{x}_1}{d\lambda }$. We can therefore write Fermat’s principle as

$$\delta OPL=\int [\left(\frac{\partial n}{\partial x_i}\delta x_i\right)\sqrt{{\dot{x}}_1^2+{\dot{x}}_2^2}+n\frac{1}{\sqrt{{\dot{x}}_1^2+{\dot{x}}_2^2}}{\dot{x}}_i\delta {\dot{x}}_i]d\lambda =0$$

To evaluate this integral we would like to integrate by parts. We can write the integrand as $$u=n\frac{1}{\sqrt{{\dot{x}}_1^2+{\dot{x}}_2^2}}{\dot{x}}_i$$

and

$$dv=\delta {\dot{x}}_{i}d\lambda$$

We can now calculate $du$ and $v$ and obtain

$$du=\frac{d}{d\lambda }\left[n\frac{1}{\sqrt{{\dot{x}}_1^2+{\dot{x}}_2^2}}{\dot{x}}_i\right]d\lambda$$

and

$$v=\delta x_i$$

With these expressions we can now apply the integration by parts formula $\int udv=uv-\int vdu$, we get:

$$\int n\frac{1}{\sqrt{{\dot{x}}_1^2+{\dot{x}}_2^2}}{\dot{x}}_i\delta {\dot{x}}_{i}d\lambda =\left[n\frac{1}{\sqrt{{\dot{x}}_1^2+{\dot{x}}_2^2}}{\dot{x}}_i\delta x_i\right]{|}_{{\lambda }_1}^{{\lambda }_2}-\int \delta x_i\frac{d}{d\lambda }\left[n\frac{1}{\sqrt{{\dot{x}}_1^2+{\dot{x}}_2^2}}{\dot{x}}_i\right]d\lambda$$

This can be substituted back into the original equation to obtain

$$\begin{array}{rl}\delta OPL& =\int \left[\left(\frac{\partial n}{\partial x_i}\delta x_i\right)\sqrt{{\dot{x}}_1^2+{\dot{x}}_2^2}\right]d\lambda \\ & +\left[n\frac{1}{\sqrt{{\dot{x}}_1^2+{\dot{x}}_2^2}}{\dot{x}}_i\delta x_i\right]{|}_{{\lambda }_1}^{{\lambda }_2}\\ & -\int \delta x_i\frac{d}{d\lambda }\left[n\frac{1}{\sqrt{{\dot{x}}_1^2+{\dot{x}}_2^2}}{\dot{x}}_i\right]d\lambda =0\end{array}$$

After rearranging the terms we get

$$\begin{array}{rl}\delta OPL& =\int \{\frac{\partial n}{\partial x_i}\sqrt{{\dot{x}}_1^2+{\dot{x}}_2^2}-\frac{d}{d\lambda }\left[n\frac{1}{\sqrt{{\dot{x}}_1^2+{\dot{x}}_2^2}}{\dot{x}}_i\right]\}\delta x_{i}d\lambda \\ & +\left[n\frac{1}{\sqrt{{\dot{x}}_1^2+{\dot{x}}_2^2}}{\dot{x}}_i\delta x_i\right]{|}_{{\lambda }_1}^{{\lambda }_2}=0\end{array}$$

and therefore finally

$$\delta OPL=\int [\left(\frac{\partial n}{\partial x_i}\right)\sqrt{{\dot{x}}_1{}^2+{\dot{x}}_2{}^2}-\frac{d}{d\lambda }\left(n\frac{1}{\sqrt{{\dot{x}}_1^2+{\dot{x}}_2^2}}{\dot{x}}_i\right)]\delta x_{i}d\lambda +\text{ boundary terms }$$

for which we choose the parameter $\lambda$ such that the boundary terms vanish.

$$\lambda =s$$

such that

$$\sqrt{{\dot{x}}_1^2+{\dot{x}}_2^2}=1$$

and finally leads to the Euler-Lagrange equation

$$\left(\frac{\partial n}{\partial x_i}\right)-\frac{d}{ds}\left(n{\dot{x}}_i\right)=0$$

which is the differential form of the Fermat’s principle.