The Wave Character of Particles
Electron diffraction and de Broglie wavelength
De Broglie proposed that if electromagnetic waves could exhibit particle-like properties, perhaps particles could demonstrate wave-like behavior. To explore this concept and determine a particle’s wavelength, he merged principles from classical mechanics with the quantum model of light. Consider a particle with mass
The quantum model of light shows us that a photon’s momentum can be written as
By combining these equations and assuming the momentum descriptions are equivalent, we can derive the wavelength for a particle:
De Broglie first published this relationship in his 1924 PhD thesis, and the particle wavelength calculated using this equation became known as the de Broglie wavelength. This revolutionary proposal suggested that the wave-particle duality observed in light might be a universal principle applying to all matter.
The basis for measurements veryfying the wave character of particles is the acceleration of charged particles. This was enabled by the development of vacumm technolgy and the invention of the electron gun by J.J. Thomson in 1897. The electron gun is a device that accelerates electrons to high speeds and directs them onto a target. The electrons are accelerated by an electric field, which is generated by a voltage difference between the cathode and the anode of the electron gun. The kinetic energy of the electrons is given by the voltage difference between the cathode and the anode. The electrons are then directed onto a target, where they can be reflected or diffracted. The reflection or diffraction of the electrons can be observed by a detector, which is placed behind the target.
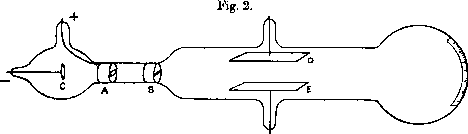
Modern accelerators can accelerators for charged particles can either be very large, such as the well known LHC at CERN, or very small an fit on a silicon chip as displayed in the image below.

Experiment by Davisson and Germer
In 1926, Davisson and Germer provided experimental proof of de Broglie’s hypothesis of matter waves by observing electron diffraction through crystalline material. In their experiment, electrons were accelerated by a voltage
where
Their key experiment involved reflecting electrons from a nickel crystal. The results are shown in the following figures:
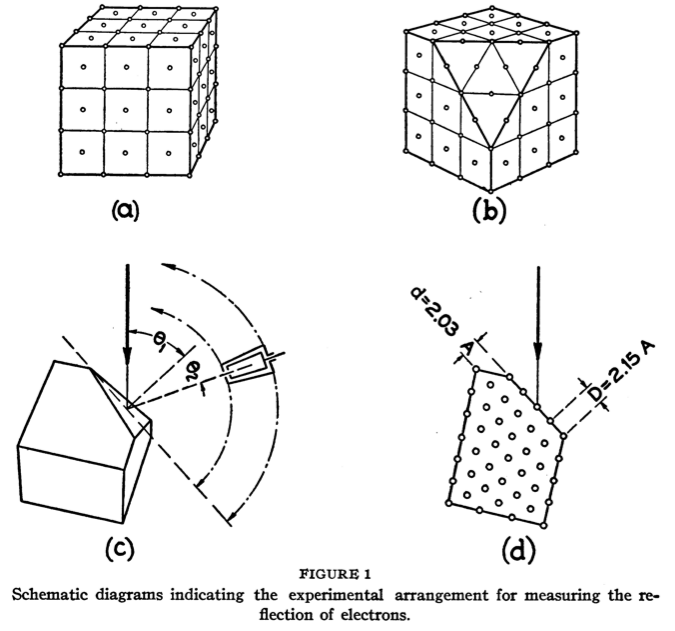
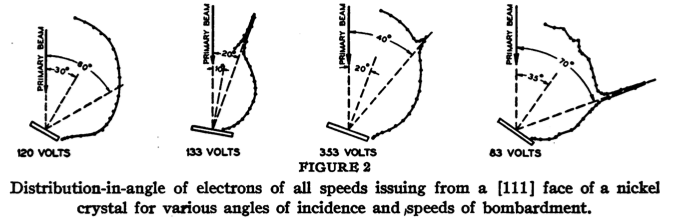
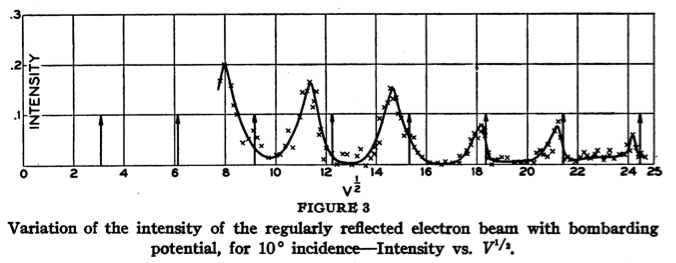
The wavelength of the electrons depends inversely on the square root of the accelerating voltage. When waves reflect on a crystal lattice, the reflection from different lattice planes can interfere constructively or destructively depending on the wavelength and angle of incidence. The sine of the reflection angle
where
Note that the angle
Combining the voltage dependence of wavelength with Bragg’s law:
Solving for the voltage giving constructive interference at angle
where
Atomic and molecular diffraction
Since then many other experiments have been carried out, which show the diffractive behavior of particles. Below are some examples of such experiments.
Atomic diffraction
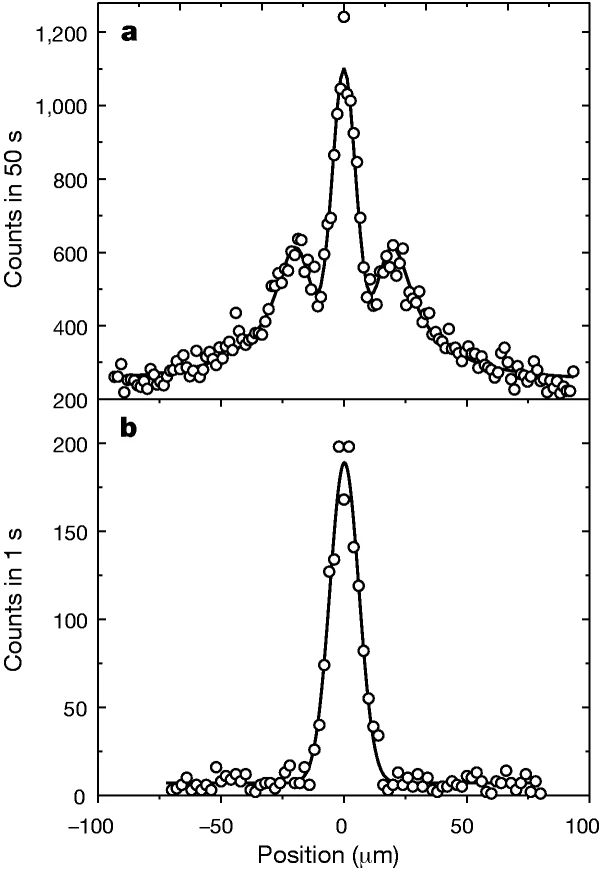
Below is an example of atomic diffraction by the group of Toennies in Göttingen from 2000. In this experiment Helium atoms were directed onto a nanofabricated grating.
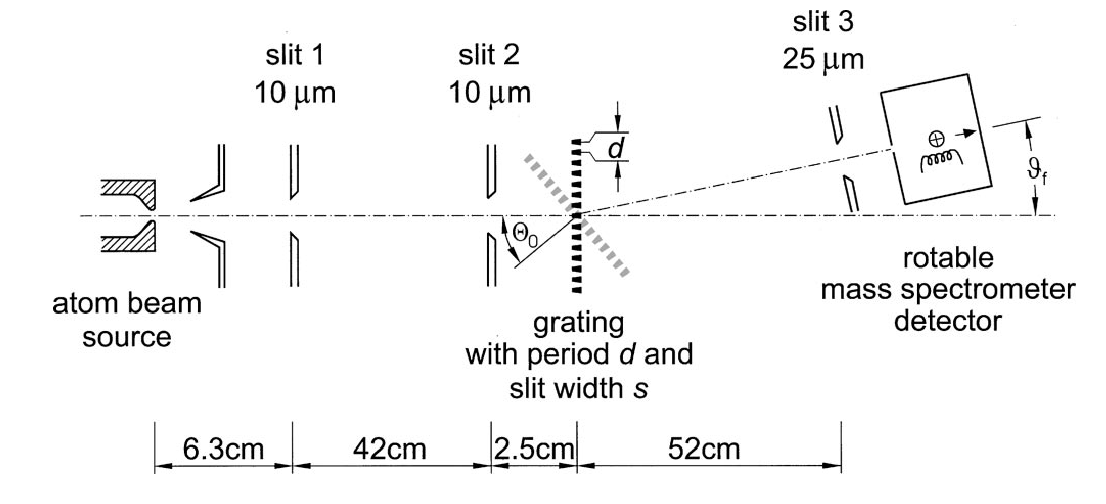
The results of this experiment are shown in the following figure.

Molecular diffraction
Experiments like that can even be extended to molecules. Below is an example for diffraction experiments in
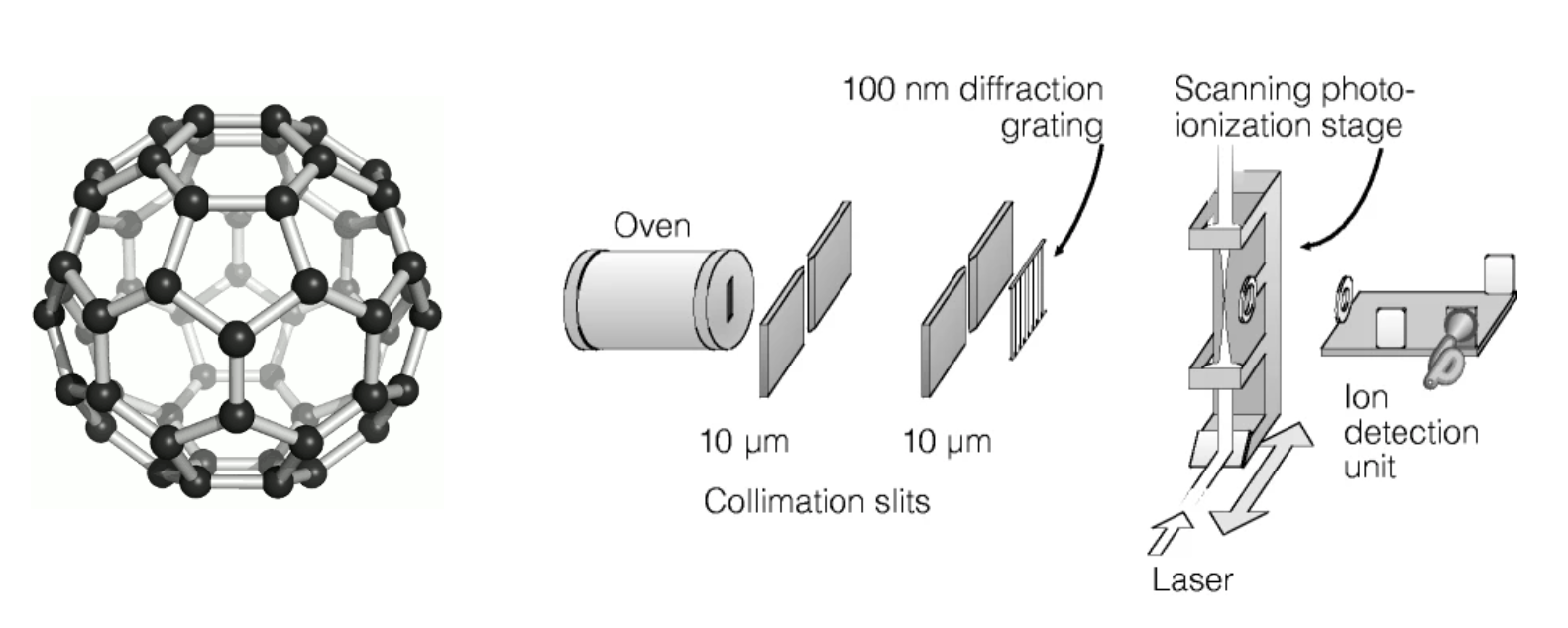
The results of this experiment are shown in the following figure.