Diffraction in Applications

Application: Diffraction in the Human Eye

The human eye provides an excellent real-world example of circular aperture diffraction through the pupil (the opening in the iris). By examining how light diffracts as it enters the eye, we can understand fundamental limits on visual resolution and how the eye is naturally optimized to these constraints.

Calculating the Diffraction Limit of the Eye

When light passes through the circular aperture of the pupil, it undergoes diffraction, producing an Airy disk pattern on the retina. The angle to the first minimum (dark ring) of the diffraction pattern is given by:

$$\sin ({\theta }_1)=0.61\frac{\lambda }{R}$$

where: - ${\theta }_1$ is the angle to the first minimum, - $\lambda$ is the wavelength of the light, - $R$ is the radius of the aperture (pupil).

For an average pupil radius of $R=2.5\text{mm}$ and green light with a wavelength of $\lambda =532\text{nm}$ (to which the human eye is most sensitive), we have:

$$\sin ({\theta }_1)=0.61\times \frac{532\times {10}^{-9}\text{m}}{2.5\times {10}^{-3}\text{m}}=0.61\times 2.128\times {10}^{-4}\approx 1.298\times {10}^{-4}$$

Thus, the angle to the first minimum is approximately:

$${\theta }_1\approx {\sin }^{-1}(1.298\times {10}^{-4})\approx {0.00744}^{\circ }$$

Determining the Size of the Airy Disk on the Retina

The distance from the pupil to the retina (the image plane) is approximately $L=20\text{mm}$ (or $2\text{cm}$). The linear radius $r$ of the Airy disk on the retina is calculated by:

$$r=L\sin ({\theta }_1)=20\text{mm}\times 1.298\times {10}^{-4}=2.596\times {10}^{-3}\text{mm}=2.596\mu \text{m}$$

So, the diameter $D$ of the Airy disk (central bright spot) is:

$$D=2r=2\times 2.596\mu \text{m}=5.192\mu \text{m}$$

This means that the smallest spot of light that can be formed on the retina due to diffraction is about $5.19\mu \text{m}$ in diameter.

Comparing with Photoreceptor Spacing in the Fovea

The fovea is a small region in the retina responsible for sharp central vision. It contains a high density of cone photoreceptor cells. The average density of cones in the fovea is approximately $150,000$ cells per square millimeter. To find the average spacing $d$ between these cells, we proceed as follows:

Area per Cell:

$$\text{Area per cell}=\frac{1{\text{mm}}^2}{150,000}=6.667\times {10}^{-6}{\text{mm}}^2=6.667\mu {\text{m}}^2$$

Linear Spacing Between Cells:

Assuming a square packing (for simplicity), the linear spacing $d$ is:

$$d=\sqrt{\text{Area per cell}}=\sqrt{6.667\mu {\text{m}}^2}\approx 2.58\mu \text{m}$$

In reality, the photoreceptors are more closely packed in a hexagonal arrangement, but this calculation gives a good approximation.

Analysis of the Results

The analysis reveals that the diameter of the Airy disk is approximately $5.192\mu \text{m}$, while the center-to-center spacing of photoreceptors in the human eye is about $2.58\mu \text{m}$. This observation is significant because the diameter of the Airy disk is roughly twice the photoreceptor spacing, indicating that the central maximum of the diffraction pattern spans about two photoreceptors.

The close correspondence between the diffraction limit of the eye and the spacing of photoreceptor cells is noteworthy for several reasons. Firstly, the diffraction limit establishes the fundamental constraint on the resolving power of the eye, determining the smallest angular separation between two points of light that can be distinguished. Secondly, the density of photoreceptors is sufficiently high to sample the details provided by the optical system up to this diffraction limit.

Increasing the density of photoreceptors within the area of the Airy disk would not enhance visual resolution due to two primary factors. The first factor is the physical limitation imposed by the diffraction limit, which is a fundamental constraint arising from the wave nature of light and the size of the pupil. Consequently, resolution cannot be improved beyond this limit merely by increasing photoreceptor density. The second factor is related to signal intensity. Adding more photoreceptors in the same area would result in each cell receiving less light, given that the total light intensity is fixed. This reduction in light per photoreceptor could potentially decrease the signal-to-noise ratio, making it more challenging to detect light.

Biological Optimization

The design of the human eye exemplifies a natural optimization process. The density of photoreceptors is matched to the optical resolving power of the eye, ensuring that the visual system extracts the maximum amount of information without unnecessary redundancy. This efficient use of resources reflects an evolutionary adaptation, where biological systems have evolved to align anatomical structures with physical laws, optimizing functions such as vision to confer survival advantages. Over time, this alignment has resulted in a visual system that is finely tuned to the constraints and capabilities imposed by the physics of light and the anatomy of the eye.

• Land, M. F., & Nilsson, D.-E. (2012). Animal Eyes (2nd ed.). Oxford University Press.
• Williams, D. R. (1988). Topography of the foveal cone mosaic in the living human eye. Vision Research, 28(3), 433–454.

Application: Resolution of an Optical Microscope

The resolution of an optical microscope is fundamentally limited by the diffraction of light as it passes through the optical components, particularly the objective lens. Diffraction causes point sources of light to produce blurred images rather than perfect points, affecting the microscope’s ability to distinguish between two closely spaced objects.

Rayleigh’s Criterion for Resolution

Key Question: How close can two point sources be while still being perceived as distinct entities by an optical system?

To answer this, we need to consider two essential aspects of how a lens modifies light:

1. Wavefront Transformation: A lens alters the curvature of incoming wavefronts, focusing parallel rays (plane waves) to a point in the focal plane.

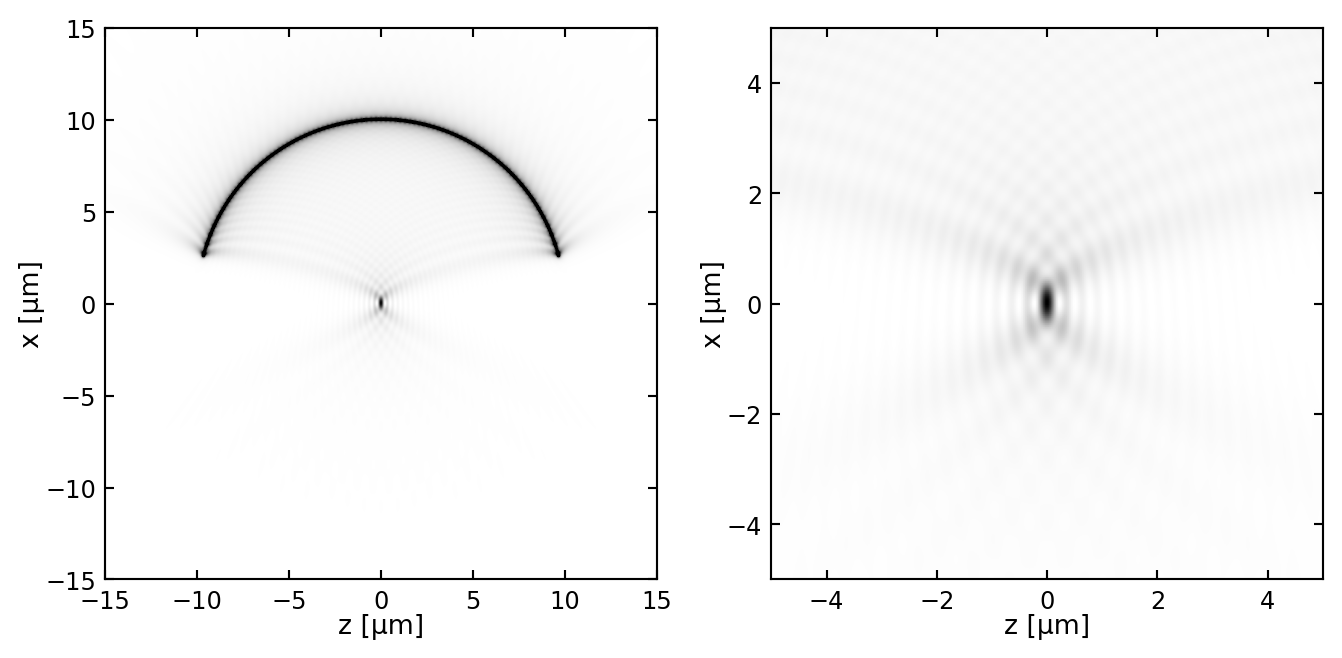
2. Finite Aperture Effects: The lens has a finite size and acts as a circular aperture, introducing diffraction effects that spread the image of a point source into a diffraction pattern known as the Airy disk.

Visual Representation:

Illustration showing two point sources and their overlapping diffraction patterns as they approach each other.

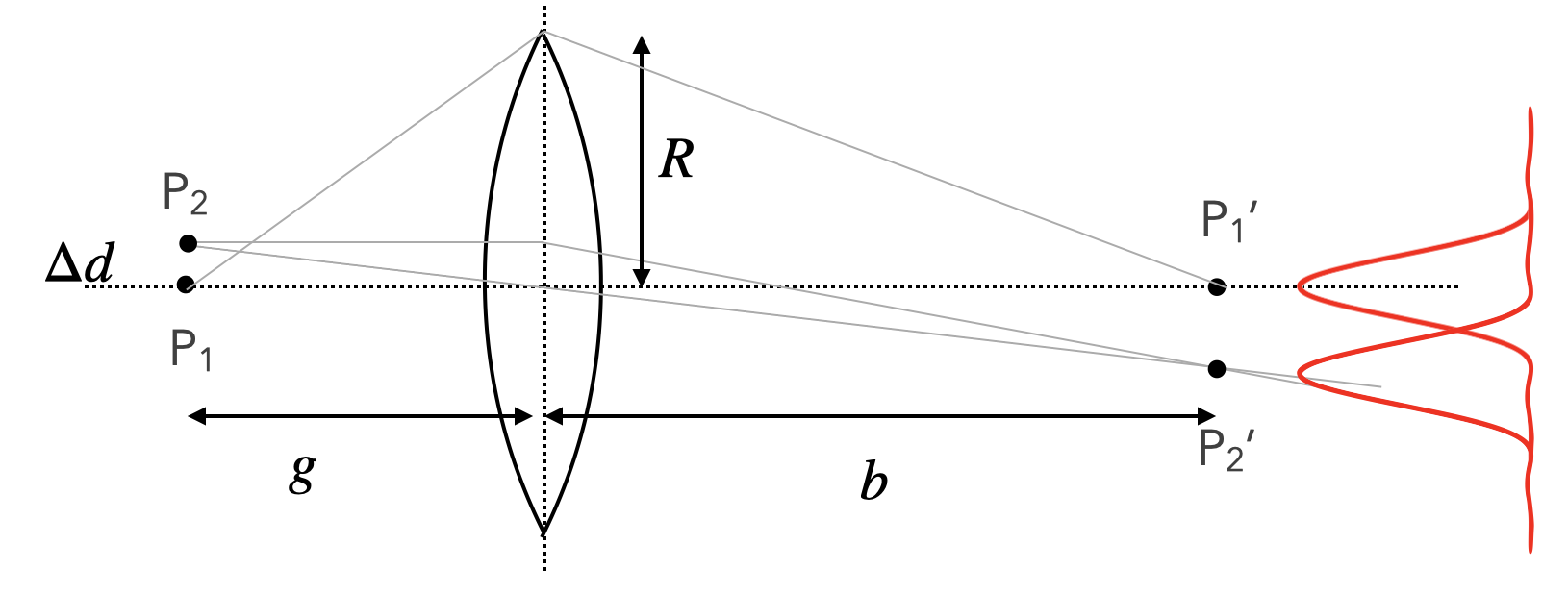
Each point source produces its own diffraction pattern. As the sources move closer, their patterns begin to overlap, making it harder to distinguish between them.

Rayleigh’s Resolution Criterion:

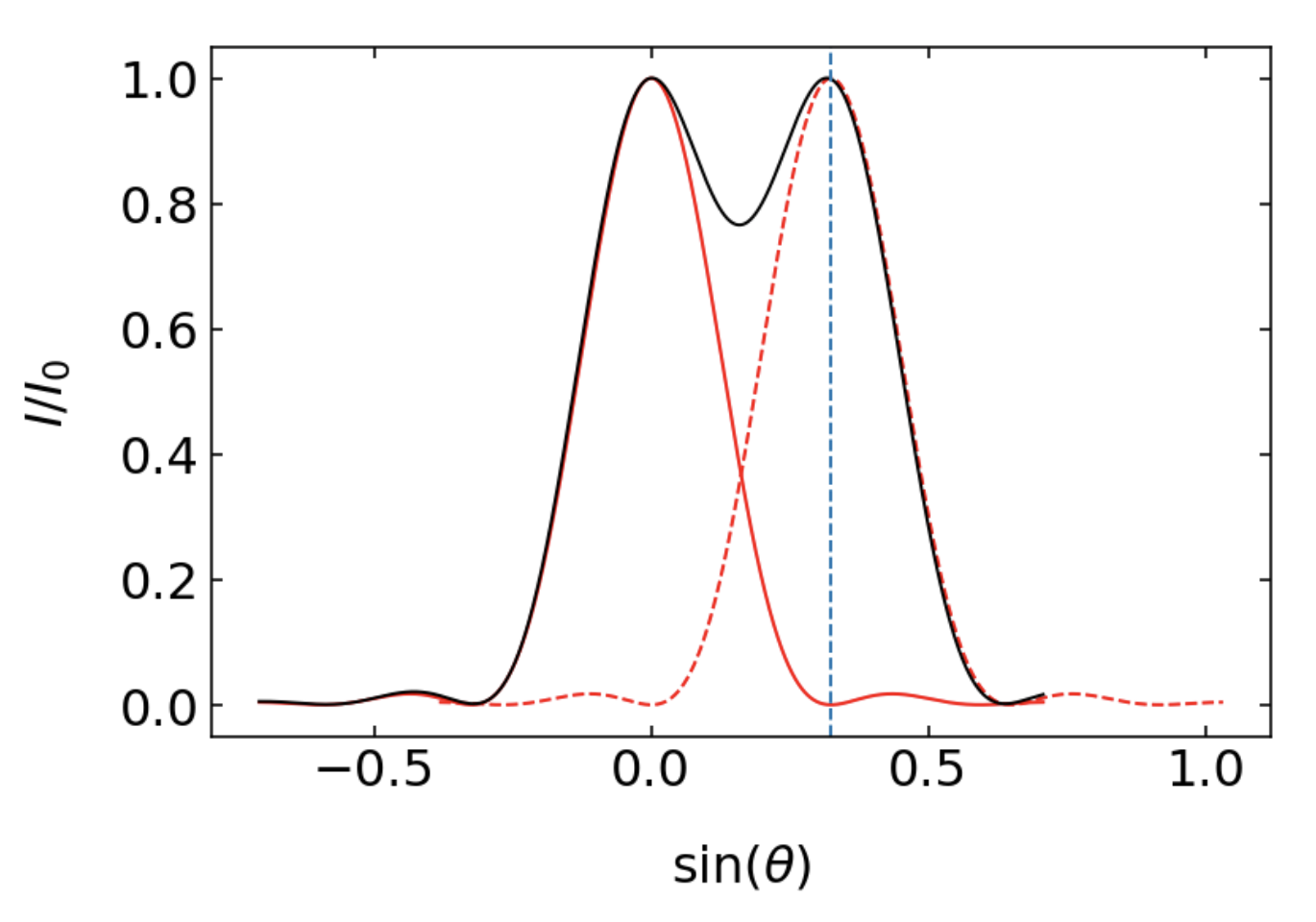
• Two point sources are considered just resolvable when the principal maximum (center) of one Airy pattern coincides with the first minimum (dark ring) of the other.

Graph depicting Rayleigh’s criterion, showing the intensity profiles of two overlapping Airy patterns.

For incoherent light sources (where the light waves are not in phase), this criterion corresponds to a 26% dip in intensity between the two peaks, which is generally sufficient for the human eye or detectors to distinguish the two sources as separate.

Angle to the First Minimum:

The angle ${\theta }_1$ to the first minimum of the diffraction pattern from a circular aperture of radius $R$ is given by:

$$\sin ({\theta }_1)=1.22\frac{\lambda }{2R}$$

Since the diameter of the aperture $D=2R$, this can also be written as:

$$\sin ({\theta }_1)=1.22\frac{\lambda }{D}$$

The factor 1.22 arises from the first zero of the Bessel function $J_1$ that describes the diffraction pattern of a circular aperture.

Small Angle Approximation:

For small angles (common in optical systems), $\sin ({\theta }_1)\approx {\theta }_1$ in radians.

Relating Angular to Linear Separation in the Image Plane:

The angular resolution ${\theta }_1$ corresponds to a linear separation $\mathrm{\Delta }x$ in the image plane (at image distance $b$):

$${\theta }_1=\frac{\mathrm{\Delta }x}{b}$$

Combining the Equations:

Substituting ${\theta }_1$:

$$\frac{\mathrm{\Delta }x}{b}=1.22\frac{\lambda }{D}$$

Solving for $\mathrm{\Delta }x$:

$$\mathrm{\Delta }x=1.22\frac{\lambda b}{D}$$

Considering the Object Plane:

The magnification $M$ of the optical system is:

$$M=\frac{b}{g}$$

where $g$ is the object distance. The corresponding separation in the object plane ($\mathrm{\Delta }d$) is:

$$\mathrm{\Delta }d=\frac{\mathrm{\Delta }x}{M}=\frac{\mathrm{\Delta }xg}{b}$$

Substituting $\mathrm{\Delta }x$:

$$\mathrm{\Delta }d=1.22\frac{\lambda b}{D}\times \frac{g}{b}=1.22\frac{\lambda g}{D}$$

Introducing Numerical Aperture (NA):

The numerical aperture (NA) of the lens is defined as:

$$\text{NA}=n\sin (\alpha )$$

where:

• $n$ is the refractive index of the medium between the object and the lens.
• $\alpha$ is the half-angle of the maximum cone of light that can enter or exit the lens.

Since $\sin (\alpha )=\frac{R}{g}$, we have:

$$D=2R=2g\sin (\alpha )$$

Substituting $D$ into $\mathrm{\Delta }d$:

$$\mathrm{\Delta }d=1.22\frac{\lambda g}{2g\sin (\alpha )}=\frac{1.22\lambda }{2\sin (\alpha )}=\frac{0.61\lambda }{\sin (\alpha )}$$

Therefore, incorporating the refractive index $n$:

$$\mathrm{\Delta }d=\frac{0.61\lambda }{n\sin (\alpha )}=\frac{0.61\lambda }{\text{NA}}$$

Under Rayleigh’s resolution criterion, several key factors influence the resolving power of an optical system.

Firstly, a higher numerical aperture (NA) improves resolution. This increase can be achieved by enhancing either the refractive index $n$ of the medium between the object and the lens or the sine of the collection angle $\sin (\alpha )$. Since the NA is defined as $\text{NA}=n\sin (\alpha )$, a larger NA allows the lens to gather more diffracted light, thereby resolving finer details in the image. In air, where the refractive index is approximately $n\approx 1$, the maximum achievable NA is less than 1, which limits the resolution. This limitation arises because the maximum value of $\sin (\alpha )$ is 1 (when $\alpha ={90}^{\circ }$), so the NA in air cannot exceed 1. In practical systems, the collection angle $\alpha$ is much less than ${90}^{\circ }$, further reducing the NA and thus the resolution. Immersion lenses, which use a medium with a higher refractive index (such as water or oil), can achieve higher NAs, overcoming this limitation and improving resolution.

Secondly, using shorter wavelengths $(\lambda )$ of light leads to better resolution. According to the formula $\mathrm{\Delta }d=\frac{0.61\lambda }{\text{NA}}$, the minimum resolvable distance $\mathrm{\Delta }d$ is directly proportional to the wavelength. Therefore, decreasing the wavelength reduces $\mathrm{\Delta }d$, allowing the optical system to distinguish smaller features of the object.

Note

Rayleigh’s Resolution Criterion

Two incoherent point sources can be resolved when their minimum separation $\mathrm{\Delta }d$ satisfies:

$$\mathrm{\Delta }d\ge \frac{0.61\lambda }{\text{NA}}$$

Where:

• $\mathrm{\Delta }d$ is the minimum resolvable distance between the two point sources.
• $\lambda$ is the wavelength of the light used for imaging.
• $\text{NA}=n\sin (\alpha )$ is the numerical aperture of the optical system.
  • $n$ is the refractive index of the medium.
  • $\alpha$ is the half-angle of the maximum cone of light entering the lens.

Abbe’s Criterion for Resolution

Limitations of Rayleigh’s Criterion:

• Rayleigh’s criterion applies to incoherent light sources, where the intensities of the diffraction patterns add directly.
• It does not fully account for the effects of coherence and interference in the imaging process.

Ernst Abbe developed a theory that considers the imaging of coherent light sources, where the phases of the waves are correlated. It emphasizes the importance of diffracted orders and spatial frequencies in the formation of images.

The key concepts in Abbe’s theory are

Diffraction Grating Analogy:

• An object with fine details can be thought of as a diffraction grating that scatters light into multiple diffraction orders.
• The ability to resolve these fine details depends on the optical system’s capacity to capture these diffracted orders.

Spatial Frequencies:

• The finer the details in the object, the higher the spatial frequency.
• High spatial frequencies correspond to larger angles in the diffraction pattern.

Optical Transfer Function:

• Describes how different spatial frequencies are transmitted through the optical system.
• An optical system with a larger NA can transmit higher spatial frequencies, improving resolution.

Following that analogy, Abbe’s criterion states that the minimum resolvable distance $\mathrm{\Delta }d$ between two points in the object plane is given by:

$$\mathrm{\Delta }d=\frac{\lambda }{2\text{NA}}$$

Rayleigh’s and Abbe’s criteria

• Abbe’s Limit:

  • $\mathrm{\Delta }d=\frac{\lambda }{2\text{NA}}$
  • Emphasizes coherent imaging and the transmission of at least two diffracted orders (zeroth and first) for resolution.

• Rayleigh’s Limit:

  • $\mathrm{\Delta }d=\frac{0.61\lambda }{\text{NA}}$
  • Based on the visibility of intensity dips in the overlapping Airy patterns of incoherent sources.

Implications in Microscopy:

Coherent Illumination:

• Techniques like phase-contrast or interference microscopy rely on coherent light.
• Abbe’s criterion is more appropriate for these methods.

Incoherent Illumination:

• Common in conventional bright-field microscopy.
• Rayleigh’s criterion provides a practical resolution limit.

Importance of Abbe’s Criterion:

• Highlights the role of interference between diffracted waves in image formation.
• Demonstrates that resolution is fundamentally limited by the wavelength of light and the NA of the system.
• Suggests that capturing higher spatial frequencies (larger NA) leads to better resolution.

Using Huygens Sources for more

The Huygens principle is a powerful tool to calculate the diffraction pattern of an aperture. The idea is to consider the aperture as a collection of point sources, which emit spherical waves. The superposition of all these waves will then give the total wave field. Below is a Python code which demonstrates the calculation of the diffraction pattern of a spherical mirror. It uses Huygens sources placed on an arc (see left). The right image shows the resulting diffraction pattern in the focal plane of the mirror.

import numpy as np
import matplotlib.pyplot as plt

def spherical_wave(k, omega, r, r0, t):
    k_norm = np.linalg.norm(k)
    d = np.linalg.norm(r - r0[:, np.newaxis, np.newaxis], axis=0)
    return np.exp(1j * (k_norm * d - omega * t)) / d

# Parameters
wavelength = 532e-9  # Wavelength in meters (green light)
k0 = 2 * np.pi / wavelength  # Wave number
c = 299792458  # Speed of light in m/s
omega0 = k0 * c  # Angular frequency
t = 0  # Time

x = np.linspace(-15e-6, 15e-6, 900)  # x-axis from -5 µm to 5 µm
z = np.linspace(-15e-6, 15e-6, 900)  # z-axis from -5 µm to 5 µm
X, Z = np.meshgrid(x, z)
r = np.array([X, np.zeros_like(X), Z])  # Observation points in 3D space (y=0)

num_sources = 100  # Number of point sources along the arc
arc_angle = np.deg2rad(100)  # Total arc angle in radians (60 degrees)
theta_sources = np.linspace(-arc_angle / 2, arc_angle / 2, num_sources)  # Source angles
radius = 10e-6  # Radius of the arc (10 µm)

total_field = np.zeros_like(X, dtype=complex)

for theta in theta_sources:
    # Calculate source position (x0, z0) on the arc
    x0 = radius * np.cos(theta)
    z0 = radius * np.sin(theta)
    r0 = np.array([x0, 0, z0])  # Source position in 3D space
    field = spherical_wave(k0, omega0, r, r0, t)
    total_field += field

intensity = np.abs(total_field)**2

intensity/=intensity[450,450]
fig,ax=plt.subplots(1,2,figsize=get_size(18, 10))

extent = [np.min(z)*1e6, np.max(z)*1e6, np.min(x)*1e6, np.max(x)*1e6]
ax[1].imshow(intensity.transpose(), extent=extent, origin='lower', cmap='gray_r',vmax=1)
ax[1].set_xlabel('z [µm]')
ax[1].set_ylabel('x [µm]')
ax[1].set_xlim(-5, 5)
ax[1].set_ylim(-5, 5)

extent = [np.min(z)*1e6, np.max(z)*1e6, np.min(x)*1e6, np.max(x)*1e6]
ax[0].imshow(intensity.transpose(), extent=extent, origin='lower', cmap='gray_r',vmax=1)
ax[0].set_xlabel('z [µm]')
ax[0].set_ylabel('x [µm]')
ax[0].set_xlim(-15, 15)
ax[0].set_ylim(-15, 15)
plt.tight_layout()
plt.show()

The pattern changes with increasing angle of the arc, which is consistent with our knowledge of the numerical aperature defining the resolution of and optical system. The changes are especially visible along the vertical axis.

import numpy as np
import matplotlib.pyplot as plt

def spherical_wave(k, omega, r, r0, t):
    k_norm = np.linalg.norm(k)
    d = np.linalg.norm(r - r0[:, np.newaxis, np.newaxis], axis=0)
    return np.exp(1j * (k_norm * d - omega * t)) / d

# Parameters
wavelength = 532e-9  # Wavelength in meters (green light)
k0 = 2 * np.pi / wavelength  # Wave number
c = 299792458  # Speed of light in m/s
omega0 = k0 * c  # Angular frequency
t = 0  # Time

x = np.linspace(-15e-6, 15e-6, 900)  # x-axis from -5 µm to 5 µm
z = np.linspace(-15e-6, 15e-6, 900)  # z-axis from -5 µm to 5 µm
X, Z = np.meshgrid(x, z)
r = np.array([X, np.zeros_like(X), Z])  # Observation points in 3D space (y=0)

num_sources = 100  # Number of point sources along the arc
arc_angle = np.deg2rad(150)  # Total arc angle in radians (60 degrees)
theta_sources = np.linspace(-arc_angle / 2, arc_angle / 2, num_sources)  # Source angles
radius = 10e-6  # Radius of the arc (10 µm)

total_field = np.zeros_like(X, dtype=complex)

for theta in theta_sources:
    # Calculate source position (x0, z0) on the arc
    x0 = radius * np.cos(theta)
    z0 = radius * np.sin(theta)
    r0 = np.array([x0, 0, z0])  # Source position in 3D space
    field = spherical_wave(k0, omega0, r, r0, t)
    total_field += field

intensity = np.abs(total_field)**2

intensity/=intensity[450,450]
fig,ax=plt.subplots(1,2,figsize=get_size(18, 10))

extent = [np.min(z)*1e6, np.max(z)*1e6, np.min(x)*1e6, np.max(x)*1e6]
ax[1].imshow(intensity.transpose(), extent=extent, origin='lower', cmap='gray_r',vmax=1)
ax[1].set_xlabel('z [µm]')
ax[1].set_ylabel('x [µm]')
ax[1].set_xlim(-5, 5)
ax[1].set_ylim(-5, 5)

extent = [np.min(z)*1e6, np.max(z)*1e6, np.min(x)*1e6, np.max(x)*1e6]
ax[0].imshow(intensity.transpose(), extent=extent, origin='lower', cmap='gray_r',vmax=1)
ax[0].set_xlabel('z [µm]')
ax[0].set_ylabel('x [µm]')
ax[0].set_xlim(-15, 15)
ax[0].set_ylim(-15, 15)
plt.tight_layout()
plt.show()