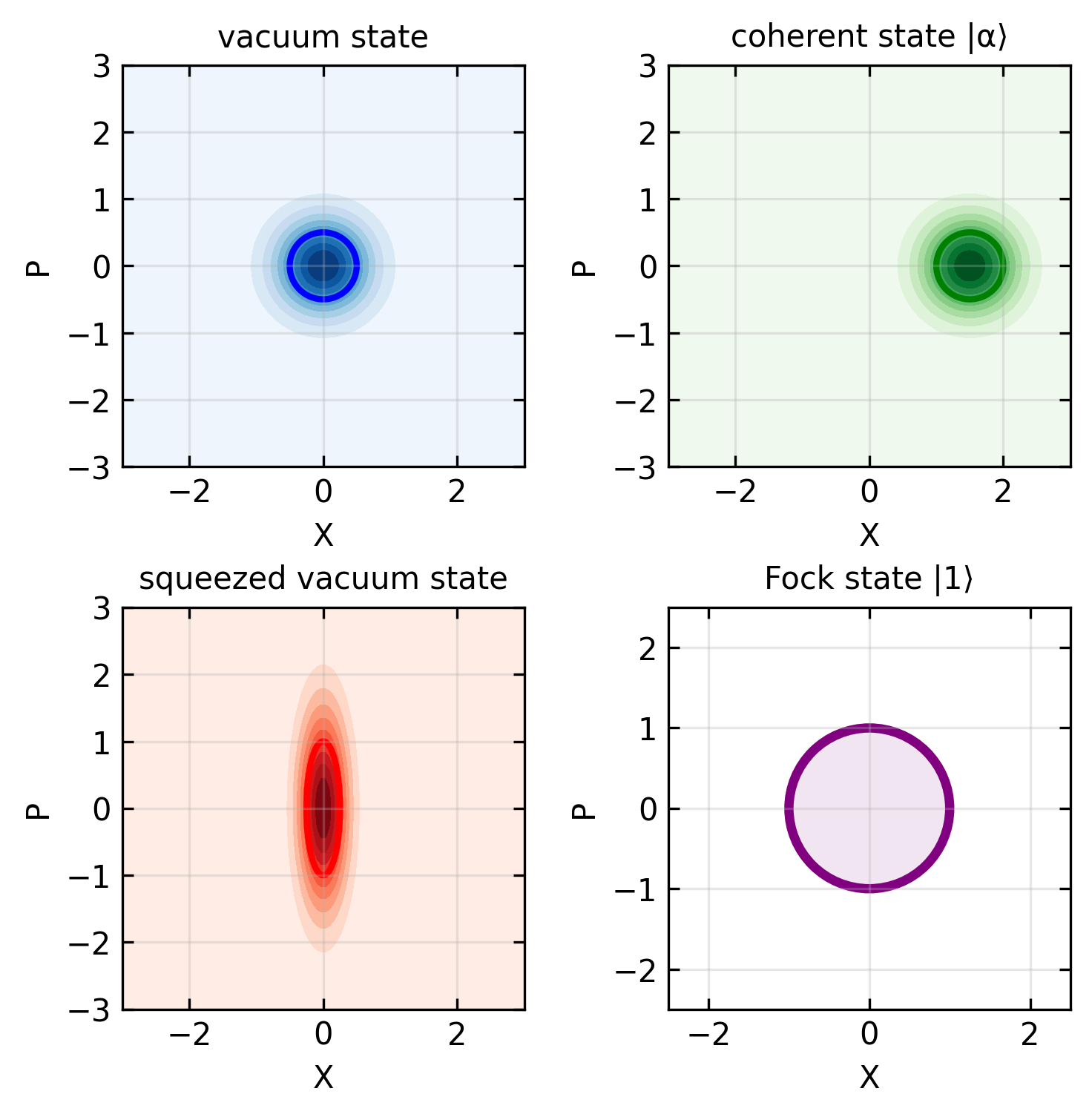
Beam Splitter Transformation
A beam splitter is a fundamental optical element that can generate quantum entanglement. Physically, it consists of a partially reflective interface (often a thin metallic layer on glass) that splits an incident beam of light into reflected and transmitted components. In quantum optics, this simple device becomes a powerful tool for creating non-classical correlations between photons.
For a beam splitter with arbitrary reflection and transmission coefficients (r and t), the transformation can be represented by a unitary matrix:
\[\begin{pmatrix} \hat{c} \\ \hat{d} \end{pmatrix} = \begin{pmatrix} t & r \\ r & -t \end{pmatrix} \begin{pmatrix} \hat{a} \\ \hat{b} \end{pmatrix}\]
where the unitarity conditions require \(|t|^2 + |r|^2 = 1\) and \(t^*r + tr^* = 0\). The most common case is a 50:50 beam splitter where \(|t|^2 = |r|^2 = 1/2\).
In the Schrödinger picture, focusing on creation operators for a 50:50 beam splitter, we have:
\[\hat{c}^\dagger = \frac{1}{\sqrt{2}}(\hat{a}^\dagger + \hat{b}^\dagger)\] \[\hat{d}^\dagger = \frac{1}{\sqrt{2}}(\hat{a}^\dagger - \hat{b}^\dagger)\]
where \(\hat{a}^\dagger\) and \(\hat{b}^\dagger\) are creation operators for the input ports, and \(\hat{c}^\dagger\) and \(\hat{d}^\dagger\) are for the output ports.
These transformations preserve the commutation relations, ensuring that \([\hat{c},\hat{c}^\dagger] = [\hat{d},\hat{d}^\dagger] = 1\) and \([\hat{c},\hat{d}^\dagger] = [\hat{d},\hat{c}^\dagger] = 0\), which can be verified by direct substitution.
The beam splitter evolution can also be described by a unitary operator that expresses how input states transform into output states:
\[\hat{U}_{BS} = \exp[\theta(\hat{a}^\dagger\hat{b}e^{-i\phi} - \hat{a}\hat{b}^\dagger e^{i\phi})]\]
This operator has a physical interpretation that directly relates to how a beam splitter works:
- The operator describes the coupling between input modes a and b that creates the mixed output state
- It represents the quantum interference process within the beam splitter that transforms input fields into output fields
- The terms \(\hat{a}^\dagger\hat{b}\) and \(\hat{a}\hat{b}^\dagger\) represent the mode mixing - they describe how the two input modes become correlated and interfere with each other inside the beam splitter
- The parameter \(\theta\) controls the splitting ratio: \(\theta = \pi/4\) gives a 50:50 beam splitter, while other values create uneven splitting
- The phase factor \(\phi\) determines the relative phase between reflection and transmission
When this unitary operator acts on an input state (such as one photon in mode a and none in mode b), it transforms the input into an output state that is a quantum superposition across both output ports. The coupling terms in the exponent are what create this superposition - they mathematically describe how the input modes interfere within the beam splitter to produce the characteristic photon distribution at the outputs.
Hong-Ou-Mandel Effect
The Hong-Ou-Mandel (HOM) effect, first demonstrated experimentally in 1987, is a quintessential quantum interference phenomenon that has no classical analog. It occurs when two identical single photons enter a 50:50 beam splitter simultaneously from different input ports. This effect provides a concrete demonstration of the mode mixing described by the beam splitter unitary operator - the coupling terms \(\hat{a}^\dagger\hat{b}\) and \(\hat{a}\hat{b}^\dagger\) in the operator create correlations between the input modes that lead to this remarkable interference behavior.
Consider a state with one photon in each input port: \(|1_a, 1_b\rangle = \hat{a}^\dagger \hat{b}^\dagger |0\rangle\).
After passing through the beam splitter, this state transforms according to the mode mixing relationships. We apply the beam splitter transformations:
\[\hat{c}^\dagger = \frac{1}{\sqrt{2}}(\hat{a}^\dagger + \hat{b}^\dagger), \quad \hat{d}^\dagger = \frac{1}{\sqrt{2}}(\hat{a}^\dagger - \hat{b}^\dagger)\]
These transformation equations encode the fundamental physics: each output mode is a quantum superposition of both input modes. The physical meaning is: - Output c receives contributions from both inputs in phase (+ sign): light from input a (transmitted) and input b (reflected) interfere constructively - Output d receives contributions from both inputs out of phase (- sign): the same pathways now have a relative phase difference that can lead to destructive interference - The 1/√2 factors ensure energy conservation and equal splitting probability - The different signs between outputs create the interference patterns that lead to quantum effects like photon bunching
Starting with the input state \(\hat{a}^\dagger \hat{b}^\dagger |0\rangle\), we need to express this in terms of the output modes. We can invert the beam splitter relations to get:
\[\hat{a}^\dagger = \frac{1}{\sqrt{2}}(\hat{c}^\dagger + \hat{d}^\dagger), \quad \hat{b}^\dagger = \frac{1}{\sqrt{2}}(\hat{c}^\dagger - \hat{d}^\dagger)\]
Substituting these into our input state:
\[\hat{a}^\dagger \hat{b}^\dagger |0\rangle = \frac{1}{\sqrt{2}}(\hat{c}^\dagger + \hat{d}^\dagger) \cdot \frac{1}{\sqrt{2}}(\hat{c}^\dagger - \hat{d}^\dagger)|0\rangle = \frac{1}{2}(\hat{c}^\dagger + \hat{d}^\dagger)(\hat{c}^\dagger - \hat{d}^\dagger)|0\rangle\]
Expanding the product:
\[= \frac{1}{2}[(\hat{c}^\dagger)^2 - \hat{c}^\dagger\hat{d}^\dagger + \hat{d}^\dagger\hat{c}^\dagger - (\hat{d}^\dagger)^2]|0\rangle\]
Since creation operators for different modes commute (\(\hat{c}^\dagger\hat{d}^\dagger = \hat{d}^\dagger\hat{c}^\dagger\)), the middle terms cancel:
\[= \frac{1}{2}[(\hat{c}^\dagger)^2 - (\hat{d}^\dagger)^2]|0\rangle\]
Simplifying and normalizing:
\[\frac{1}{\sqrt{2}}(|2_c, 0_d\rangle - |0_c, 2_d\rangle)\]
This is an entangled state where both photons exit together through the same output port, with equal probability of finding both photons in either output. Remarkably, the probability of finding one photon in each output port is zero—a purely quantum effect known as the Hong-Ou-Mandel effect or photon bunching. This bunching behavior emerges directly from the mode mixing: the quantum interference created by the beam splitter’s coupling of input modes results in destructive interference for the “one photon per output” amplitude, while constructive interference occurs for the “both photons in same output” amplitudes.
To appreciate how unusual this behavior is, consider two identical red balls rolling toward a fork in the road. Classically, each ball would randomly choose one path or the other, and sometimes they’d separate. But quantum mechanically, if these were photons, they would always choose the same path. This photon bunching arises from their bosonic nature and quantum interference.
Experimentally, the HOM effect is observed by varying the relative arrival time of the two photons at the beam splitter using a delay line. When the photons arrive at different times, they behave independently, and coincidence detections occur 50% of the time. However, as the temporal overlap increases, the coincidence rate drops, reaching zero for perfectly indistinguishable photons. This creates the characteristic “HOM dip” in the coincidence count rate:
\[R_c(\Delta t) = R_0\left(1 - V\exp\left(-\frac{(\Delta t)^2}{2\sigma^2}\right)\right)\]
where \(V\) is the visibility (ideally 1 for perfect indistinguishability) and \(\sigma\) relates to the coherence time of the photons.
The HOM effect serves as:
- A highly sensitive method to measure timing differences down to femtoseconds
- A test of photon indistinguishability in all degrees of freedom (frequency, polarization, spatial mode)
- A fundamental building block for linear optical quantum computing
- A tool for characterizing single-photon sources
Phase-Based Understanding and Quantum Paths
The HOM effect can be understood more intuitively through probability amplitudes and the concept of indistinguishable paths.
For a 50:50 beam splitter with energy conservation and time-reversal symmetry, there are two common phase conventions in the literature:
Convention 1 (Phase on Transmission - used here): - Reflection amplitude: \(r = 1/\sqrt{2}\) (real) - Transmission amplitude: \(t = i/\sqrt{2}\) (π/2 phase shift)
Convention 2 (Phase on Reflection - also common): - Reflection amplitude: \(r = i/\sqrt{2}\) (π/2 phase shift) - Transmission amplitude: \(t = 1/\sqrt{2}\) (real)
Both conventions are physically correct and lead to identical experimental predictions. The choice depends on the specific beam splitter design (dielectric vs metallic coating), measurement reference frame, and theoretical convenience. The essential physics is that one of the two processes (reflection or transmission) must acquire a π/2 phase shift to satisfy unitarity and energy conservation. We use Convention 1 in this analysis.
Connection to Fresnel Equations: The phase factors in quantum beam splitters have their origin in classical electromagnetic theory through the Fresnel equations. When light reflects from or transmits through an interface, the Fresnel equations predict phase shifts that depend on: - The refractive indices of the materials - The angle of incidence - The polarization of the light
For a dielectric beam splitter (like a glass plate with metallic coating), the Fresnel equations can predict phase shifts of 0, π/2, or π depending on the specific geometry and materials. However, the quantum beam splitter phase conventions are often chosen for mathematical convenience rather than direct correspondence to the Fresnel phases. The key constraint is that the beam splitter matrix must be unitary, which requires a specific phase relationship between reflection and transmission amplitudes.
In practice, real beam splitters may have phase shifts that don’t exactly match either convention due to: - Coating properties and thickness - Wavelength dependence - Angular dependence - Substrate effects
For quantum optics calculations, we typically use the idealized phase conventions and then account for real device characteristics through calibration measurements when necessary.
With two photons entering from different ports, four possible pathways must be considered:
Photon from port a reflects to port c, photon from port b reflects to port d:
- Amplitude = \(r \cdot r = 1/2\)
- Final state: \(|1_c, 1_d\rangle\)
Photon from port a transmits to port d, photon from port b transmits to port c:
- Amplitude = \(t \cdot t = (i/\sqrt{2})^2 = -1/2\)
- Final state: \(|1_c, 1_d\rangle\)
Both photons exit from port c (one reflects, one transmits):
- Amplitude = \(r \cdot t = i/2\)
- Final state: \(|2_c, 0_d\rangle\)
Both photons exit from port d (one reflects, one transmits):
- Amplitude = \(t \cdot r = i/2\)
- Final state: \(|0_c, 2_d\rangle\)
The critical quantum interference occurs between pathways 1 and 2, which lead to the same final state \(|1_c, 1_d\rangle\). The total amplitude for this outcome is:
\[A_{|1_c, 1_d\rangle} = r^2 + t^2 = 1/2 + (-1/2) = 0\]
This perfect destructive interference explains why one photon is never observed in each output port.
For the bunched outcomes, the amplitudes are:
\[A_{|2_c, 0_d\rangle} = rt = i/2\] \[A_{|0_c, 2_d\rangle} = tr = i/2\]
Squaring these amplitudes gives the probabilities:
- Probability of one photon in each output port: \(|0|^2 = 0\)
- Probability of both photons in port c: \(|i/2|^2 = 1/4\)
- Probability of both photons in port d: \(|i/2|^2 = 1/4\)
When normalized (multiplying by 2), there is a 50% probability for each bunched outcome.
Generalizations and Applications
The beam splitter entanglement mechanism extends beyond the two-photon case. For example, with input state \(|n_a, m_b\rangle\), the output becomes a complex superposition of states \(|k_c, (n+m-k)_d\rangle\) weighted by binomial coefficients.
The beam splitter’s entangling capabilities are utilized in:
Bell state generation: By placing a source of entangled photon pairs (e.g., from spontaneous parametric down-conversion) at one input port and vacuum at the other, beam splitters can help prepare specific Bell states for quantum communication protocols.
Quantum teleportation: Beam splitters are essential components in Bell-state analyzers used for quantum teleportation, where they create the necessary entanglement between photons.
Boson sampling: A computational problem where multiple photons are sent through a network of beam splitters, creating a complex entangled state whose photon statistics are believed to be classically hard to simulate.
Quantum metrology: HOM interference enables quantum-enhanced measurements that can exceed classical precision limits, particularly in quantum imaging and sensing applications.
The quantum interference at a beam splitter thus represents one of the most elegant demonstrations of quantum mechanics, where the simple act of splitting a beam reveals the profound wave-particle duality of light and generates entanglement—a uniquely quantum resource with no classical analog.