This page was generated from `/home/lectures/exp3/source/notebooks/L10/MultiWave Interference.ipynb`_.

Multiple Wave Interference

Multiple Wave Interference with Decreasing Amplitude

We will turn our attention now to a slight modification of the previous multiwave interference. We will introduce a decreasing amplitude of the individual waves. The first wave shall have an amplitude $U_1=\sqrt{I_0}$. The next wave, however, will not only be phase shifted but also have a smaller amplitude.

$$U_2=h{U}_1$$

where $h=r{e}^{i\varphi }$ with $|h|=r<1$. $r$ can be regarded as a reflection coefficient, which deminishes the amplitude of the incident wave. According to that the intensity is reduced by

$$I_2=|U_2{|}^2=|h{U}_1{|}^2=r^2{I}_1$$

The intensity of the incident wave is multiplied by a factor $r^2$, while the amplitude is multiplied by $r$. Note that the phase factor $e^{i\varphi }$ is removed when taking the square of this complex number.

Intensity at Boundaries

The amplitude of the reflected wave is diminished by a factor $r\le 1$, which is called the reflection coefficient. The intensity is diminished by a factor $R=|r{|}^2\le 1$, which is the reflectance.

In the absence of absorption, reflectance $R$ and transmittance $T$ add to one due to energy conservation.

$$R+T=1$$

Consequently, the third wave would be now $U_3=h{U}_2=h^2{U}_1$. The total amplitude is thus

$$U=U_1+U_2+U_3+\dots +U_M=\sqrt{I_0}(1+h+h^2+\dots )$$

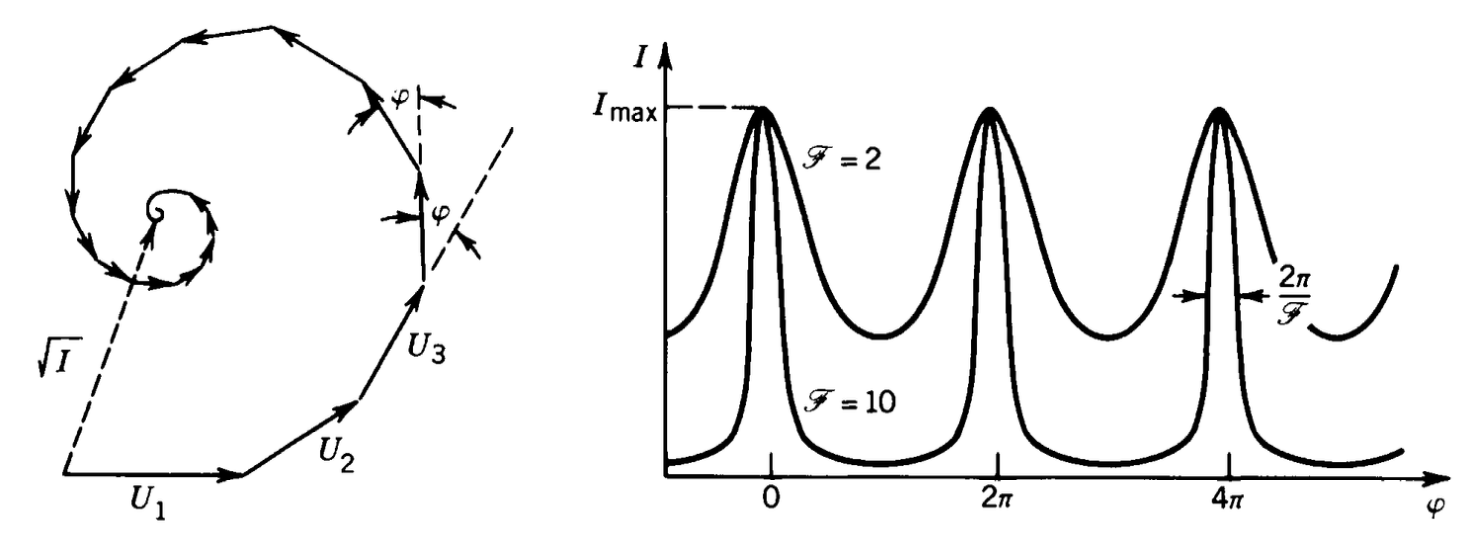
Fig.: Multiple wave interefence with decreasing amplitudes. Left: Phase construction of a multiwave intereference with M equal amplitude waves. Right: Intensity distribution obtained as a function of the phase shift $\varphi$.

This yields again

$$U=\sqrt{I_0}\frac{(1-h^M)}{1-h}=\frac{\sqrt{I_0}}{1-r{e}^{i\varphi }}$$

Calculating the intensity of the waves is giving

$$I=|U{|}^2=\frac{I_0}{|1-r{e}^{i\varphi }{|}^2}=\frac{I_0}{(1-r{)}^2+4r{\sin }^2(\varphi /2)}$$

which is also known as the Airy function. This function can be further simplified by the following abbrevations

$$I_{\mathrm{m}\mathrm{a}\mathrm{x}}=\frac{I_0}{(1-r{)}^2}$$

and

$$\mathcal{F}=\frac{\pi \sqrt{r}}{1-r}$$

where the latter is called the Finesse. With those abbrevations, we obtain

$$I=\frac{I_{\mathrm{m}\mathrm{a}\mathrm{x}}}{1+4\left(\frac{\mathcal{F}}{\pi }\right){\sin }^2(\varphi /2)}$$

for the interference of multiple waves with decreasing amplitude.

This intensity distribution has a different shape than the one we obtained for multiple waves with the same amplitude.

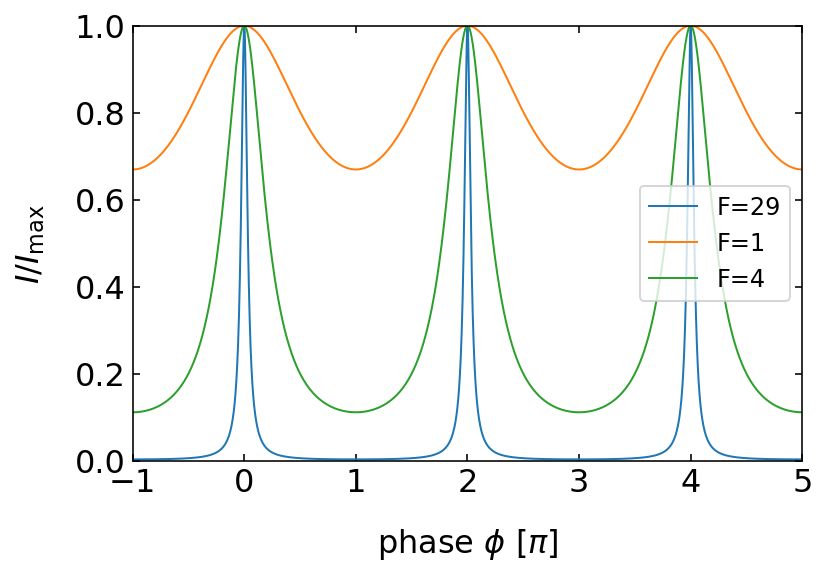
Fig.: Multiple wave interference with decreasing amplitude. The graph shows the intensity distribution over the phase angle $\varphi$ for different values of the Finesse $\mathcal{F}$.

We clearly observe that with increasing Finesse the intensity maxima, which occur at multiples fo $\pi$ get much narrower. In addition the regions between the maxima show better contrast and fopr higher Finesse we get complete destructive interference.