This page was generated from `/home/lectures/exp3/source/notebooks/L2/Optical Elements I.ipynb`_.

Optical Elements Part I

## just for plotting later

import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
%config InlineBackend.figure_format = 'retina'

plt.rcParams.update({'font.size': 12,
                     'axes.titlesize': 18,
                     'axes.labelsize': 16,
                     'axes.labelpad': 14,
                     'lines.linewidth': 1,
                     'lines.markersize': 10,
                     'xtick.labelsize' : 16,
                     'ytick.labelsize' : 16,
                     'xtick.top' : True,
                     'xtick.direction' : 'in',
                     'ytick.right' : True,
                     'ytick.direction' : 'in',})

Mirrors

Plane Mirrors

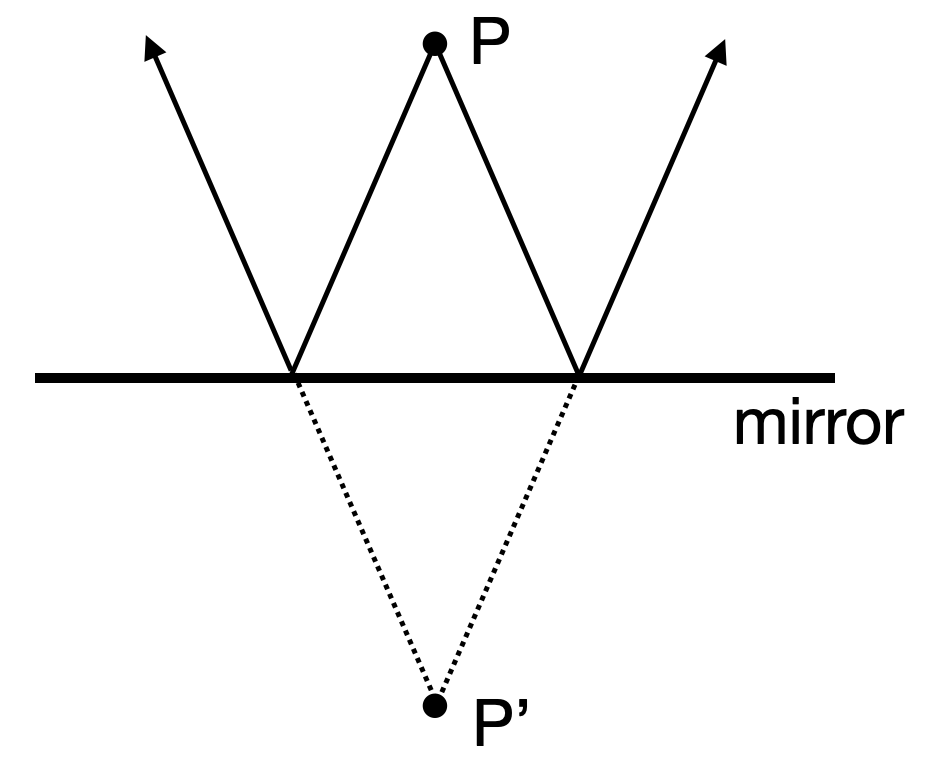
If a point \(P\) send out light that is reflected on a mirror as depicted in the image below, the rays reflected from the mirror diverge, but appear to originate from a point \(P^\prime\) behind the mirror. The distance of this image point from the mirror is the same as the one of the object point from the mirror due to the reflection law. An observer, who would thus collect all the reflected rays and image them e.g. onto the retina of his eye will see the point behind the mirror.

Fig.: Image formation on a plane mirror.

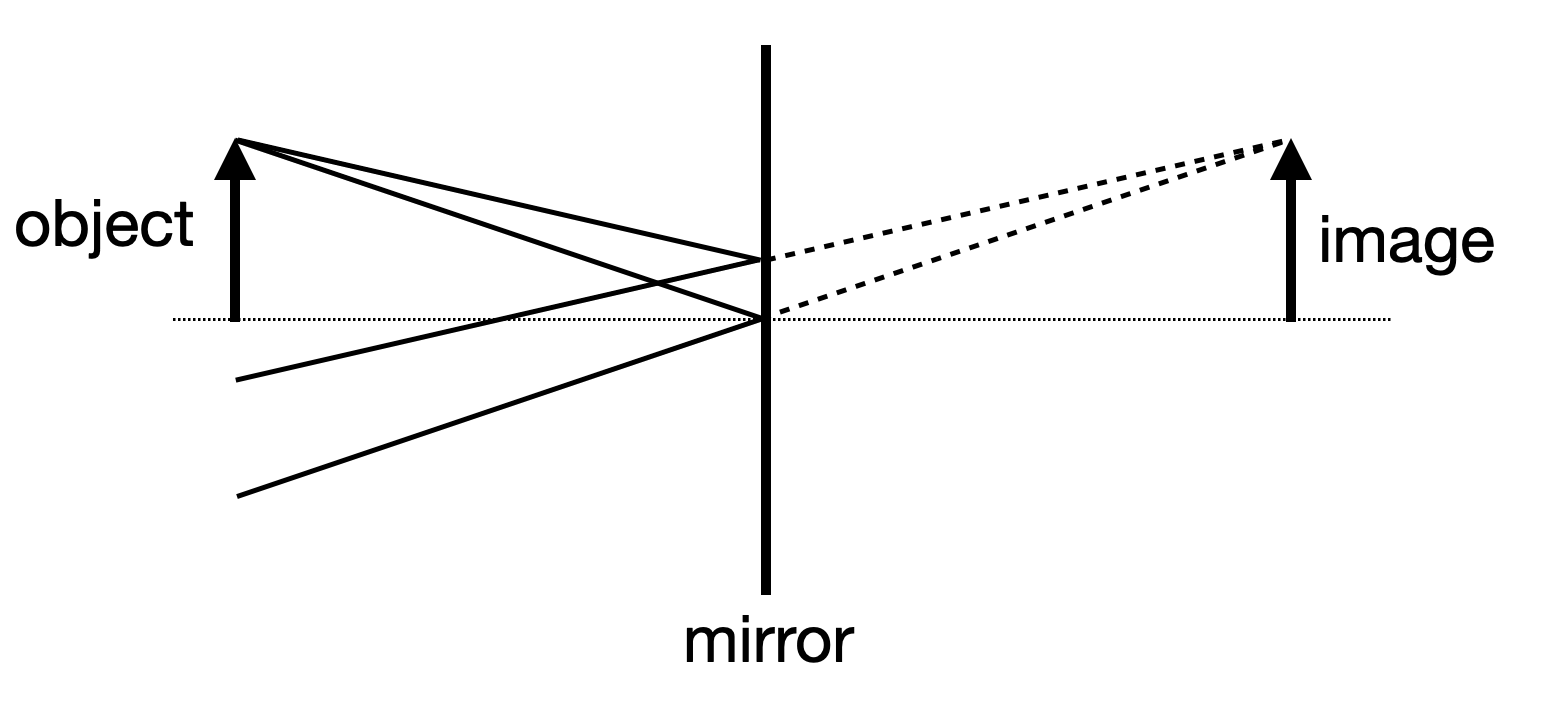
If now many point of an object emit light towards the mirror then this is also true for all of the points and the whole object appears as an image behind the mirror. Consequently, the image has the same size than the object. Therefore the magnification defined as

\begin{equation} M=\frac{h_{\rm image}}{h_{\rm object}}=1 \end{equation}

Fig.: Image formation on a plane mirror.

Concave Mirrors

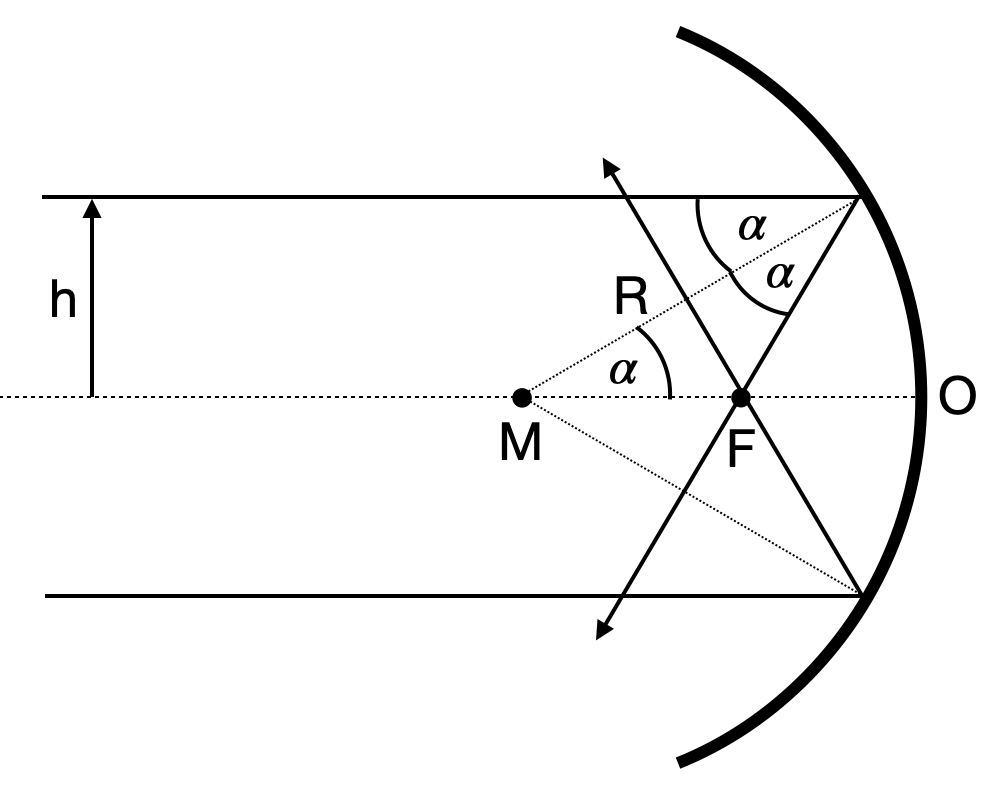
When we apply the law of reflection for a concave mirror (i.e. the reflecting side of the mirror is on the inside of the spherical surface), the light parallel to the optical axis at a distance \(h\) is reflected towards the optical axis and crosses the axis at a specifc point \(F\). For symmetry reasons, a ray on the other side of the mirror needs to cross the axis in the same point.

Fig.: Ray propagation on a concave mirror.

We may calculate the position of the point \(F\), e.g. the distance from the mirror surface point \(O\), by applying the law of reflection. If the spherical mirror surface has a radius \(R\), then the distance between the center of the sphere \(M\) and the point \(F\) is given by

\[FM=\frac{R}{2\cos(\alpha)}\]

Therefore, we can also calculate the distance of the mirror surafce from the point \(F\), which results in

\begin{equation} OF=R\left (1-\frac{1}{2\cos(\alpha)}\right)=f \end{equation}

This distance is the so-called focal length of the concave mirror \(f\). For small angle \(\alpha\), the above equation yields the so called paraxial limit (all angles are small and the rays are close to the optical axis). In this limit we find \(\cos(\alpha)\approx 1\) and the focal length becomes \(f=R/2\). If we replace the cosine function by \(\cos(\alpha)=\sqrt{1-sin^2(\alpha)}\) with \(\sin(\alpha)=h/R\), we find

\begin{equation} f=R\left [ 1-\frac{R}{2\sqrt{R^2-h^2}}\right ] \end{equation}

This equation is telling us, that the focal distance is not a single value for a concave mirror. The focal distance rather changes with the distance \(h\) from the optical axis. If \(h\) approaches \(R\) the focal length become shorter.

To obtain now an equation which predicts the point at which the reflected ray intersects the optical axis if it emerged at a point \(A\), we just consider the following sketch.

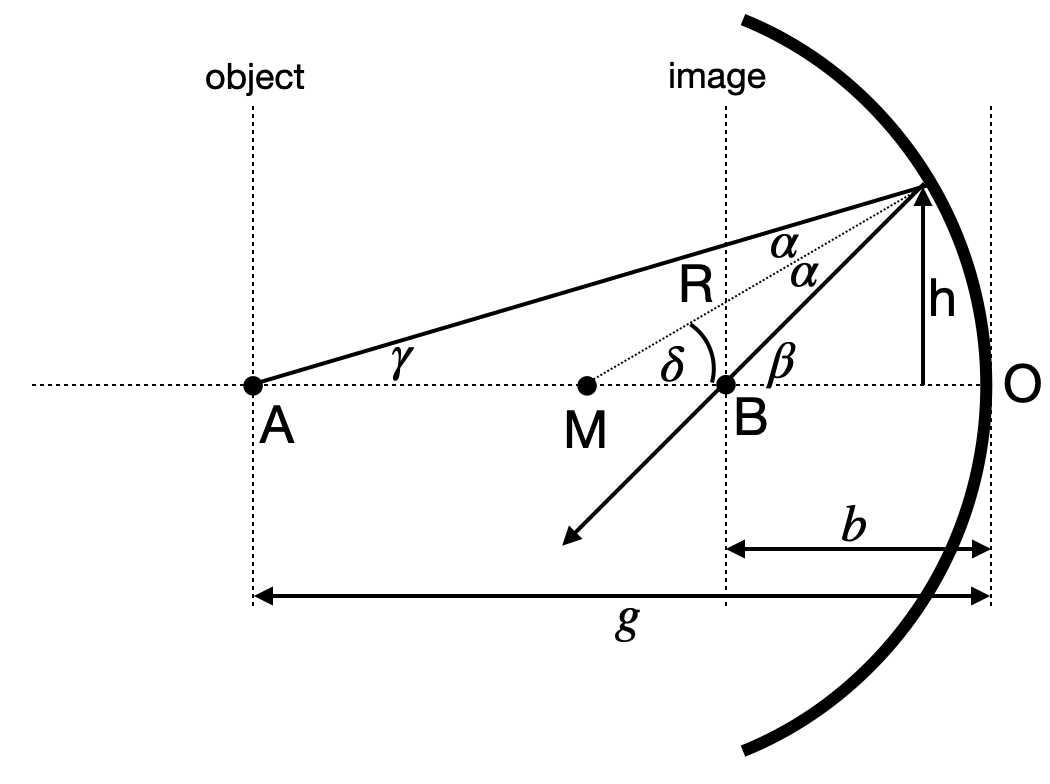
Fig.: Image formation on a concave mirror.

For this situation, we can write down immediately the following relations

\[\delta=\alpha+\gamma\]

\[\gamma+\beta=2\delta\]

Further

\[\tan(\gamma)=\frac{h}{g}\approx \gamma\]

and

\[\tan(\beta)=\frac{h}{b}\approx \beta\]

and finally

\[\sin(\delta)=\frac{h}{R}\approx \delta\]

from which we obtain the imaging equation

\[\frac{1}{g}+\frac{1}{b}\approx \frac{2}{R}\approx \frac{1}{f}\]

This equation has some surprising property. It is completely independent of \(h\) and \(\gamma\). That means all points in a plane at a distance \(g\) are images into a plane at a distance \(b\). Both planes are therefore called conjugated planes.

Imaging Equation Concave Mirror

The sum of the inverse object and image distances equals the inverse focal length of the cocave mirror.

\[\frac{1}{g}+\frac{1}{b}\approx\frac{1}{f}\]

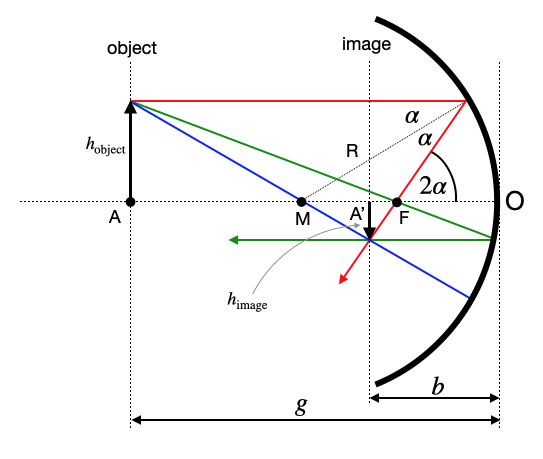
This equation now helps to construct the image of an object in front of a concave mirror and we may define 3 different rays to identify the size of an image \(h_{\rm image}\) from the size of an object \(h_{\rm object}\).

Fig.: Image formation on a concave mirror.

In the above sketch, there are three different rays, which help us to construct the image.

1. red ray: parallel ray → focal ray

2. green ray: focal ray → parallel ray

3. central ray: central ray → central ray

All three reflected rays will either intersect on the same side of the mirror as the object. In this case, the image is called real image and it will be inverted as in the sketch. If the reflected rays on the other hand diverge, the appear to intersect behind the mirror. In this case, the image is called virtual image. It is located behind the mirror. There is no real intersection of rays in that case.

The intersection point further gives the size of the image. Using a ray from the tip of the object to the intersection between mirror and optical axis (O), we may easily determine the image height \(h_{\rm image}\). Try yourself, if you see that the magnification of a concave mirror is described by

\[\frac{h_{\rm image}}{h_{\rm image}}=-\frac{b}{g}=M\]

As mentioned earlier, this resembles to be the magnification \(M\). The minus sign in the ratio of image and object distance appears due to the fact that the image is reversed in its orientation in a real image.

With the help of the imaging equation and the magnification we may in general differentiate between the following general situations:

1. \(g>2f\): image is real, inverted and smaller than the object

2. \(g=2f\): image is real, inverted and of the same size than the object

3. \(f<g<2f\): image is real, inverted and larger than the object

4. \(g<f\): image is virtual, upright and larger than the object