This page was generated from `/home/lectures/exp3/source/notebooks/L22_AMA/Particle_character_of_light.ipynb`_.

The Particle Character of Light

The photoelectric effect

In 1888 Wilhelm Hallwachs published an experiment with charged foils connected to a metal plate which was irradiated with ultraviolet light (we did this experiment in the last lecture before Christmas). If the foils and the plate are negatively charged and electrically isolated against the surrounding, the charge do decrease upon irradiation with ultraviolet light. In constrast, if the system is positively charged, the charge does not decrease. Hallwachs concluded that the light is responsible for negative charges leaving the metal plate.

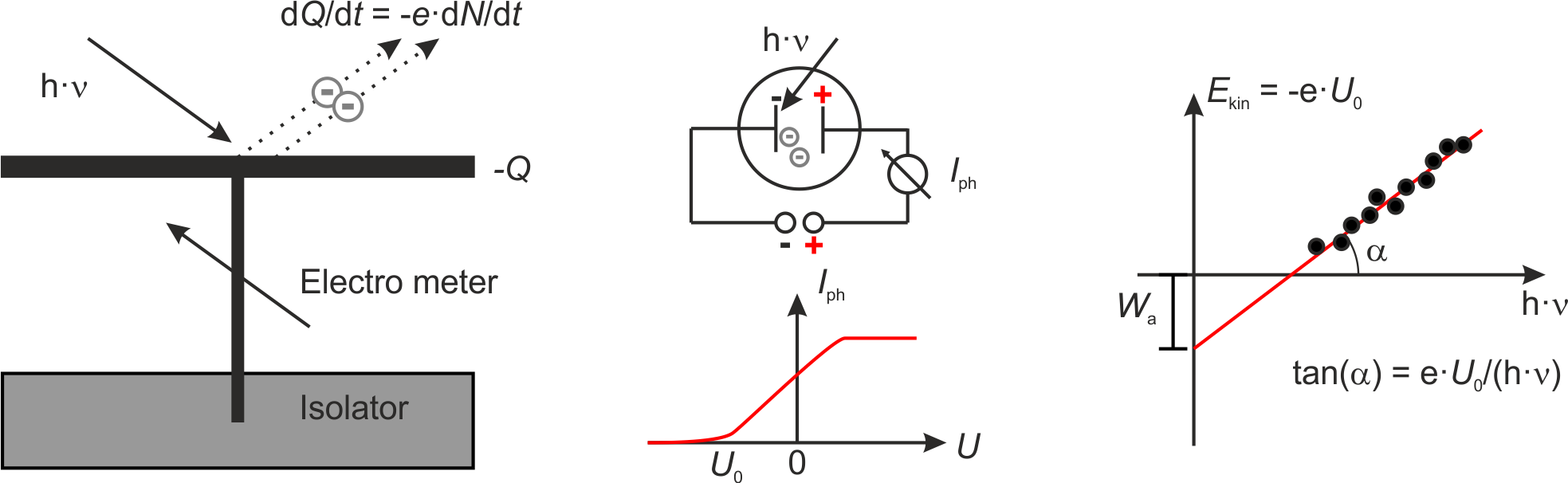
Fig.: (left) Scheme of the apparatus used by Hallwachs. (center) Scheme of the apparatus used by Lennard and the corresponding photocurrent :math:`I_{mathrm{ph}}`. (right) From the onset voltage :math:`U_0` one can calculate the work function :math:`W_{mathrm{a}}` as intercept and Planck’s constant :math:`h` as part of the slope.

Later in 1902 Lennard measured the photocurrent between two plates in vacuum. The current set in already at a negative voltage \(U_0\) between the plates, incresed with rising voltage, and reached a plateau which depended only on the light’s intensity. He concluded:

• The electrons must bear a minimum energy in order to overcome the oppositely directed electric field, \(E_{\mathrm{kin}} \le e \cdot U_0\).

• The kinetic energy \(m v^2/2\) of the photoelectrons depends on the frequency \(\nu\) of the light, not on the light’s intensity.

• The number of photoelectrons is proportional to the light’s intensity.

• There is no delay between light irradiation and electron emission.

In 1905 Einstein successfully explained these findings on the basis of the quantum model of light. In accord to this model every absorbed photon transfers its energy \(h \cdot \nu\) completely to one electron. The maximum kinetic energy of an electron is then governed by

\[E_{\mathrm{kin}}^{\mathrm{max}} = h \cdot \nu - W_{\mathrm{a}} \mathrm{,}\]

with \(W_{\mathrm{a}} = -e \left( \phi_{\mathrm{vac}} - \phi \right)\) being the work function of the cathode material (often the vacuum work function is set to zero, \(\phi_{\mathrm{vac}} = 0\). The work function is the amount of energy one has to compensate in order to bring one electron from bulk into vacuum against the forces binding the electron in bulk.

Since one can determine the maximum kinetric energy \(E_{\mathrm{kin}}^{\mathrm{max}} = -e\cdot U_0\) (\(U_0 < 0\)) from the voltage \(U_0\) at which the photocurrent set in and

\[-e\cdot U_0 = h\cdot\nu - W_{\mathrm{a}} \mathrm{,}\]

one is able to determine the work function on teh basis of the intercept of the \(-e\cdot U_0\) vs. \(h\cdot\nu\) curve and Planck’s constant from the slope of the curve.

If we assume (against one’s better knowledge) a fully wave-like behavior of light, then light with a radiation power of \(P_{\mathrm{L}}\) might hit a surface with an area \(A\) and shares its energy equally between all electrons. For a penetration depth of \(\Delta z \approx \lambda\) and a density of the conducting electrons of \(N\), then every conducting electron gets on average the energy of

\[\bar{\Delta W} = \frac{P_\mathrm{L}}{N \cdot A \cdot \lambda} \; \Delta t\]

within the time interval \(\Delta t\). Thus, the work function can be compensated in the case of

\[\Delta t > W_{\mathrm{a}} \; \frac{N \cdot A \cdot \lambda}{P_\mathrm{L}} \mathrm{.}\]

Let us consider a zinc plat with a work function of \(W_{\mathrm{a}} = 4 \, \mathrm{eV}\) and a light source with a spectral filter \(\lambda = 250 \; \mathrm{nm}\) emitting a power of \(P_\mathrm{L} = 1 \; \mathrm{W}\) at a distance of \(R = 1 \; \mathrm{m}\) away from our zinc plate, there will an intensity of

\[I_{\mathrm{L}} = \frac{P_\mathrm{L}}{4\pi R^2} \approx 8\cdot 10^{-6} \; \frac{\mathrm{W}}{\mathrm{cm}^{-2}}\]

reaching the plate. For a penetration depth of \(\Delta z \approx \lambda\) this intensity will be distrubuted between

\[N = 10^{23} \cdot \mathrm{cm}^{-3}\cdot \lambda = 2.5 \cdot 10^{18} \; \frac{1}{{\mathrm{cm}^{-2}}}\]

electron, whereas each electron acquires on average a power of

\[P_{\mathrm{el}} = 3 \cdot 10^{-24} \; \mathrm{W} = 2 \cdot 10^{-5} \; \mathrm{eVs}^{-1} \mathrm{.}\]

Thus, it will take a time of \(\Delta t = W_{\mathrm{a}}/P_{\mathrm{el}} = 2 \cdot 10^5 \; \mathrm{s}\) for one electron to acquire enough energy to leave the zinc plate. This result is in clear contrast to experiemntal findings.

One example for an experiment proving Einstein’s explanation of the photoeffect was provided by von Joffé und Dobronrawov in 1925. They used small, charged bismuth beads holded within a Millikan capacitor and irradiated those beads with low-dose X-rays. Every change of the overall charge of the beads interfere the equilibrium in the capacitor, and can be observed by means of a change of the bead position. Using a radiation power of \(P = 10^{-12} \; \mathrm{W}\) meaning an emission rate of \(\dot{N} = 10^3\) photons per second with an energy of \(h \cdot \nu = 10^4 \; \mathrm{eV}\) on average every 30 minutes a change of the bead charge was detected. The number of photons arriving at one bead within a time intervall \(\Delta t\) is \(Z = \dot{N} \cdot \Delta t \cdot \mathrm{d} \Omega/ \left( 4\pi \right)\), whith \(\mathrm{d} \Omega\) as the solid angle covered by the bead. The calculated time constant of \(Z\) was in well agreement with the observed rate of the charge alterarion. If we again assume a wave-like explanation of teh photoeffect, the emitted power within the according solid anngle will be absorbed by the bead and distributed between all its elctrons. As a consequnce the bead as a whole will have collected enough energy in order release an electron within the same period of time. However it cannot be explained how all \(10^{12}\) atoms are supposed to combine their energy in one, sinblge electron at the very same time.

The Compton effect

Another example for demonstrating the corpuscle (particle-like) character of light is the Compton effect. If an arbitrary material is irradiated with X-rays of wavelength \(\lambda_0\), one can detetct scattered light with the same wavelength \(\lambda_0\) but also scattered light with a greater wavelength \(\lambda_{\mathrm{S}} > \lambda_0\). Moreover, the wavelength of the scattered light seemes to depend much stronger on the scattering angle than on the scattering material.

This phenomenon can be explained by means of the photon model and inelastic impact. Every photon bears an energy of \(E = h \cdot \nu = \hbar \cdot \omega\) and a momentum of \(p = h/\lambda = \hbar \cdot k\). If a photon impacts into a weakly bound electron with a binding energy much smaller than the photon energy (\(E_\mathrm{B} \le E\)), we can neglect the binding energy and assume the electron as free electron. In addition we simplify further and assume the electron as beeing at rest. During the collision event

\[h \nu_0 + \mathrm{e}^{-} \longrightarrow h \nu_{\mathrm{S}} + \mathrm{e}^{-} + E_{\mathrm{kin}}\]

energy and momentum are conserved. The law of conservation of energy then reads as

\[h \, \nu_0 = h \, \nu_\mathrm{s} + E_{\mathrm{kin}}^{\mathrm{e}}\]

with \(E_{\mathrm{kin}}^{\mathrm{e}}\) as teh relativistic kinitic energy of the electron

\[E_{\mathrm{kin}}^{\mathrm{e}} = \frac{m_0 c^2}{\sqrt{1-\beta^2}} - m_0 c^2\]

and \(\beta = v/c\). If we ascribe a momentum like

\[\vec{p} = \hbar \, \vec{k}\]

with

\[\left| \vec{p} \right| = \hbar \, \left| \vec{k} \right| = h \frac{1}{\lambda}\]

to the photon, we can formulate teh law of momentum conservation as follow,

\[\hbar \, \vec{k_0} = \hbar \, \vec{k_{\mathrm{s}}} + \vec{p^{\mathrm{e}}}\]

with

\[\vec{p^{\mathrm{e}}} = \frac{m_0 \vec{v}}{\sqrt{1-\beta^2}} \mathrm{.}\]

If we isolate the square of the momentum of the electron, we obtain an equation depending of teh squared difference between the wavevectors of the incident and scattered photon. Calculating this difference leads to a scalar product between these two vectors and necessitates the introduction of the angle between the propagation direction of the incident and scattered photon. We denote thsi angle as \(\phi\),

\[\begin{split}\begin{eqnarray} \frac{m_0^2 v^2}{1-\beta^2} & = & \hbar^2 \left( \vec{k_0} - \vec{k_{\mathrm{s}}} \right)^2\\ {} & = & \hbar^2 \left( k_0^2 + k_{\mathrm{s}}^2 + 2 k_0 k_{\mathrm{s}} \cos \left( \varphi \right) \right)^2\\ {} & = & \frac{h^2}{c^2} \left( \nu_0^2 + \nu_{\mathrm{s}}^2 + 2 \nu_0 \nu_{\mathrm{s}} \cos \left( \varphi \right) \right)^2 \end{eqnarray}\end{split}\]

From the law of energy conservation we get

\[\frac{m_0^2 v^2}{1-\beta^2} = \frac{h^2}{c^2} \left( \nu_0 - \nu_{\mathrm{s}} \right)^2 + 2 h m_0 \left( \nu_0 - \nu_{\mathrm{s}}\right) \mathrm{,}\]

which we can compare with the law of momentum conservation and get

\[\nu_0 - \nu_{\mathrm{s}} = \frac{h}{m_0 c^2} \, \nu_0 \, \nu_{\mathrm{s}} \, \left(1- \cos \left( \varphi \right) \right) \mathrm{.}\]

Now making use of \(1- \cos \left( \varphi \right) = 2 \sin^2 \left( \varphi/2 \right)\) and \(\nu = c/\lambda\) we achieve the Compton formula

\[\begin{split}\begin{eqnarray} \lambda_{\mathrm{S}} & = & \lambda_0 + 2 \frac{h}{m_0 c} \sin^2 \left( \varphi/2 \right)\\ {} & = & \lambda_0 + 2 \lambda_{\mathrm{C}} \sin^2 \left( \varphi/2 \right)\\ \end{eqnarray}\end{split}\]

with \(\lambda_{\mathrm{C}}\) denoting the Compton wavelength of the electron,

\[\lambda_{\mathrm{C}} = \frac{h}{m_0 c} = 2.4262 \cdot 10^{-12} \; \mathrm{m.}\]

The Compton wavelength is a constant and represents the change of the wavelength \(\Delta \lambda = \lambda_{\mathrm{S}} - \lambda_0\) at a scattering angle of \(\varphi = 90^{\circ}\). Results from experiements almost perfectly coincide with the Compton formula. Furthermoren the ratio between the wavelengths

\[\frac{\lambda_{\mathrm{S}}}{\lambda_0} = \frac{h \nu_0}{m_0 c^2}\]

represents the ratio between the energy of the incident photon and the energy of the electron at rest. Thus, if we know the mass of the electron, we can detremine \(\varphi\) and \(\lambda_{\mathrm{S}}\) (and therefor \(\lambda_{\mathrm{C}}\)) and calculate \(h\).

Properties of photons

During the 18th century there was a dispute about the nature of light. Newton proposed a particle-like character on the basis of the straight propagation and the law of refraction. In contrast, Huygens proposed a wave-like character of light on the basis of interference and diffraction. This interpretation seemed to be proven when Heinrich Hertz discovered electromagnetic waves and light was interpreted as a special spectral region being as well governed by Maxwell’s equations. As we have seen on the basis of the experiemnts, light –and more general electromagnetic waves– might show corpuscular characteristics as well. That is why we have to introduce a particle-like description in additon to the allready known wave-like description.

Energy and momentum

Every electromagnetic field consists of quanta of energy \(h \cdot \nu\), which we call photons. If we remember back for the cavity resonator, we can now state the energy density of the electromagnetic field \(\omega_{\mathrm{em}}\) as the density of modes \(n\) multiplied with the quantum of energy \(h \cdot \nu\)

\[\omega_{\mathrm{em}} = n \cdot h \cdot \nu \mathrm{.}\]

We can further comprehend the flux \(I = \varepsilon_0 c E^2\) of an electromagnetic wave as a particle flux \(\dot{N}\) of photons

\[I = \dot{N} h \nu\]

with \(\dot{N} = n \cdot c\). Therefore, if a light wave with a flux of \(I\) is shining on an area is tantamount with a particle flux of photons reaching this area.

As demonstrated on the basis of the Comptopn effect, every photon bears a momentum \(\vec{p} = \hbar \cdot \vec{k}\) with the magnitude \(\left| \vec{p} \right| = p = h \nu / c\). As a consequence, if we are able to assign an energy density to the denisty of modes, we are also able to assign a momentum density,

\[\pi_{\mathrm{em}} = n \cdot \hbar \cdot k \mathrm{.}\]

Then, the relation between the energy density \(\omega_{\mathrm{em}}\) of an electromegnatic wave and the momentum density \(\pi_{\mathrm{em}}\) of the very same wave reads as

\[\omega_{\mathrm{em}} = c \cdot \pi_{\mathrm{em}} {.}\]

Angular momentum

Concerning the angular momentum of photons, if a free atom absorbs a photon, the angular momentum of the atom is altered by \(\hbar\). Thus, the law of the conservation of the angular momentum predicts that a photon does have an angular momentum of \(\hbar\), independent of its energy \(h \cdot \nu\). If left-handed circular polarized light (\(\sigma^{+}\) propagating along \(z\) is absorbed by a free atom, its angular momentum \(J_z\) is changed by \(\Delta J_z = + \hbar\). In the case of right-handed circular polarized light (\(\sigma^{-}\)), the change of the angular momentum of the electron is negative \(\Delta J_z = - \hbar\). We can conclude, that for \(\sigma^{+}\)-polarized light the vector of the angular momentum is oriented along the direction of propagation, whereas for \(\sigma^{-}\)-polarized light the vector of the angular momentum is oriented against the direction of propagation. Since the direction of propagation is determined through the wavevector, we can conclude for the photon’s angular momentum

\[\vec{L}_{Ph} = \pm \hbar \, \frac{\vec{k}}{\left| \vec{k} \right|}\]

Linearly polarized light can be comprehended as superposition of \(\sigma^{+}\)- and \(\sigma^{-}\)-polarized light to equal parts. Thus the angular momentum of linearly polarized light adds up to \(0\).

Mass and gravitational force

From theory of relativity we know that the mass is actually affected through the traveling speed of the reference systems, namely

\[m = \frac{1}{\sqrt{1-\left( \frac{v}{c}\right)^2}} \, m_0 \mathrm{.}\]

Furthermore, it is evedent that only particles with a mass at rest of \(m_0 = 0\) are capable to travel with the speed of light, and thus a photon does have a mass at rest of \(0\). For the energy it follows

\[\begin{split}\begin{eqnarray} E & = & \sqrt{p^2c^2 + m_0^2 c^4}\\ {} & = & p c\\ {} & = & \frac{h}{\lambda} c\\ {} & = & h \nu \end{eqnarray}\end{split}\]

in accordance with energy and momentum considerations stated above. If we now ascribe a mass \(m\) to the photon with

\[m = \frac{E}{c^2} = \frac{h \nu}{c^2}\]

and let this photon travel within a gravitational field, then the photon has to perform work in order to change its position from \(\vec{r_1}\) with the gravitational potential \(\Phi \left( \vec{r_1} \right)\) to position \(\vec{r_2}\) with the gravitational potential \(\Phi \left( \vec{r_2} \right)\). The work within teh gravitational field reads as

\[W = m \cdot \Delta \Phi = \frac{h \nu}{c^2} \left( \Phi \left( \vec{r_2} \right) - \Phi \left( \vec{r_1} \right) \right) \mathrm{.}\]

For reasons of conservation of energy, the energy of the photon \(h\cdot\nu\) has to change about the same amout the photon does perform work, and hance its frequency has to change

\[\nu_2 = \nu_1 \left(1-\frac{\Delta \phi}{c^2} \right)\]

and

\[\frac{\Delta \nu}{\nu} = \frac{\Delta \Phi}{c^2} \mathrm{.}\]

Even though a photon does not have any mass at rest, a photon experiences a red shift (longer wavelength, smaller frequency, smaller energy), if it rises within a gravitational field. The energy decrease of the photon is equal to an increase in potential energy of \(m \Delta \Phi\) with \(m = h \nu /c^2\).