This page was generated from `/home/lectures/exp3/source/notebooks/L15/Dispersion and Absorption.ipynb`_.

Dispersion and Absorption

We would like to have a closer look at what happens with our atom in the electric field of a light wave. First of all, our toy atom is very small (around 0.1 nm) which is much smaller than the wavelength of ligth (500 nm). Thus the electric field appears to homogeneous over the cross section of the atom and seems to change over time with \(E(t)=E_0 e^{-i\omega t}\).

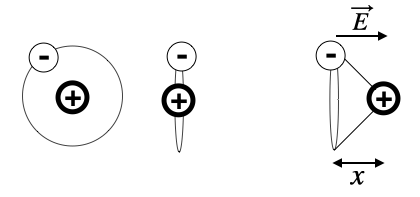
Fig.: Polarization of an electric cloud of an atom.

Lets assume the electric field being aligned with the x-direction, then we can write down the equation of motion for the displacement of the two charges in the atom

\[\ddot{x}+\sigma\dot{x}+\omega_0x=\frac{q}{m}E(t)\]

which is the equation of motion for a damped driven harmonic oscillator. Using our knowledge from the mechanical oscillator and the drivig electric field, we can use a solution

\[x(t)=x_0 e^{i\omega t}\]

and insert that into the equation of motion to get the amplitude \(x_0\). This yields

\[x(t)=\frac{1}{\omega_0^2+i\omega\sigma-\omega^2}\frac{q}{m}E(t)\]

This time dependent displacement creates a dipole moment \(p=q x(t)=\alpha E(t)\). Here \(\alpha\) is the electronic polarizability of the atom. With the help of the dipole moment we can calculate the polarization density

\[P=Nq\frac{1}{\omega_0^2+i\omega\sigma-\omega^2}\frac{q}{m}E(t)=\epsilon_0\chi E(t)\]

from which we may infer the electronic suceptibility

\[\chi=\chi_0\frac{1}{\omega_0^2+i\omega\sigma-\omega^2}\]

with

\[\chi_0=\frac{q^2N}{m\epsilon_0}\]

The susceptibility is therefore a complex number, which may write as \(\chi=\chi^{'}+i\chi^{"}\). From this it also directly follows that the dielectric function \(\epsilon_r=1+\chi\) is a complex number and the refractive index as well.

For the refractive index we can therefore write

\[n=n_r-i\kappa=\sqrt{\epsilon_r}=\sqrt{1+\chi}\]

where the minus sign between the real and imaginary part is a definition and sometimes handled differently. For the refractive index we may therefore write

\[n=1+\frac{Nq^2}{2\epsilon_0 m}\frac{(\omega_0^2-\omega^2)-i\sigma\omega}{(\omega_0^2-\omega^2)^2+\omega^2\sigma^2}=n-i\kappa\]

The refractive index therefore has a real and imaginary part, which we can derive from the above formuala. We would like to a have a look at the consequences of those two coefficients \(n_r,\kappa\) for the propagation of the light wave.

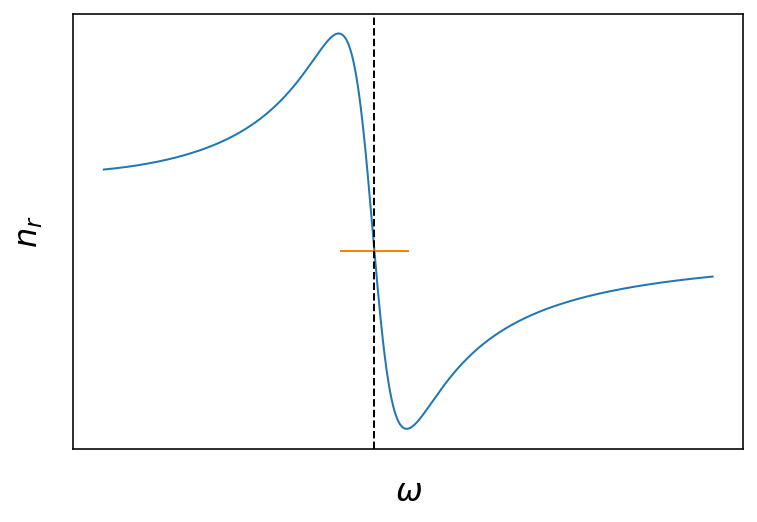
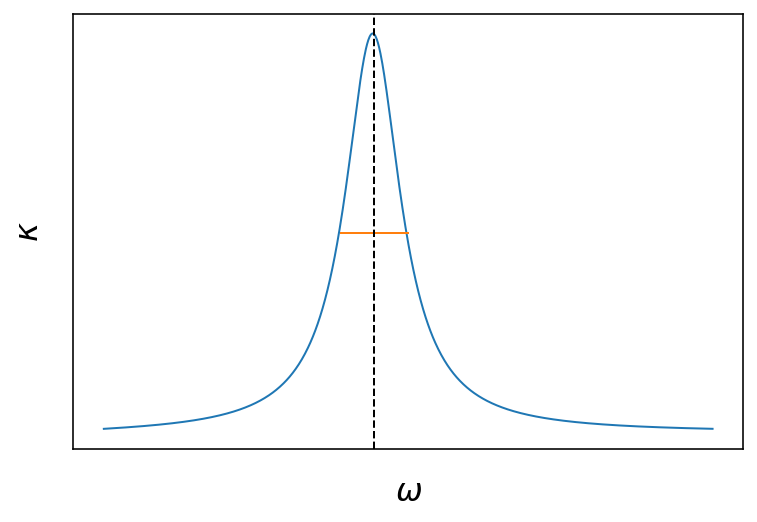
Fig.: Real and imaginary part of the refractive index as a function of the frequency. The vertical dashed line is located at \(\omega=\omega_0\).

The two plots above show the frequency dependence of the real and imaginary part of the refractive index. The freuency dependence arises from the coupling to the resonance of the damped harmonic oscillator of our crude atomic model . Around the resonance, the are strong changes to be expected for the real part and the imaginary part. The real part has a dispersive shape being larger than 1 at lower frequencies and smaller than one (!) above the resonance. The imaginary part has the shape of a Lorentzian curve around the resonance frequency, where the full width at half maximum (FWHM) of the curve us given by the damping coefficient \(\sigma\).

Absorption

We will first analyze the effect of \(\kappa\), which is the imaginary part of the refractive index.

\[E(z)=Ee^{-ik z}=E_0e^{-in k_0 z}\]

Inserting the complex refractive index yields

\[E(z)=E_0e^{-i(n-i\kappa) k_0 z} =E_0 e^{-i n_r k_0 z}e^{-\kappa k_0 z}\]

The imaginary part is creating a new real factor, which is inducating an electric field amplitude, that decays with the distance.

If we calculate the intensity we find

\begin{eqnarray} I &=& \epsilon_0 c E^2=\epsilon_0 c \left | E_0 e^{-in_r k_0 z }e^{-\kappa k_0 z} \right |^2\\ &=& e^{-2\kappa k_0 z}=e^{-\alpha z} \end{eqnarray}

where \(\alpha=2k_0 z\) is the absorption coefficient. The intensity of the wave is therefore decaying exponentially with the distance \(z\) and the corresponding law for the relative intensity

\[\frac{I}{I_0}= e^{-\alpha z} \tag{Lambert Beer Law}\]

is called Lambert-Beers law.

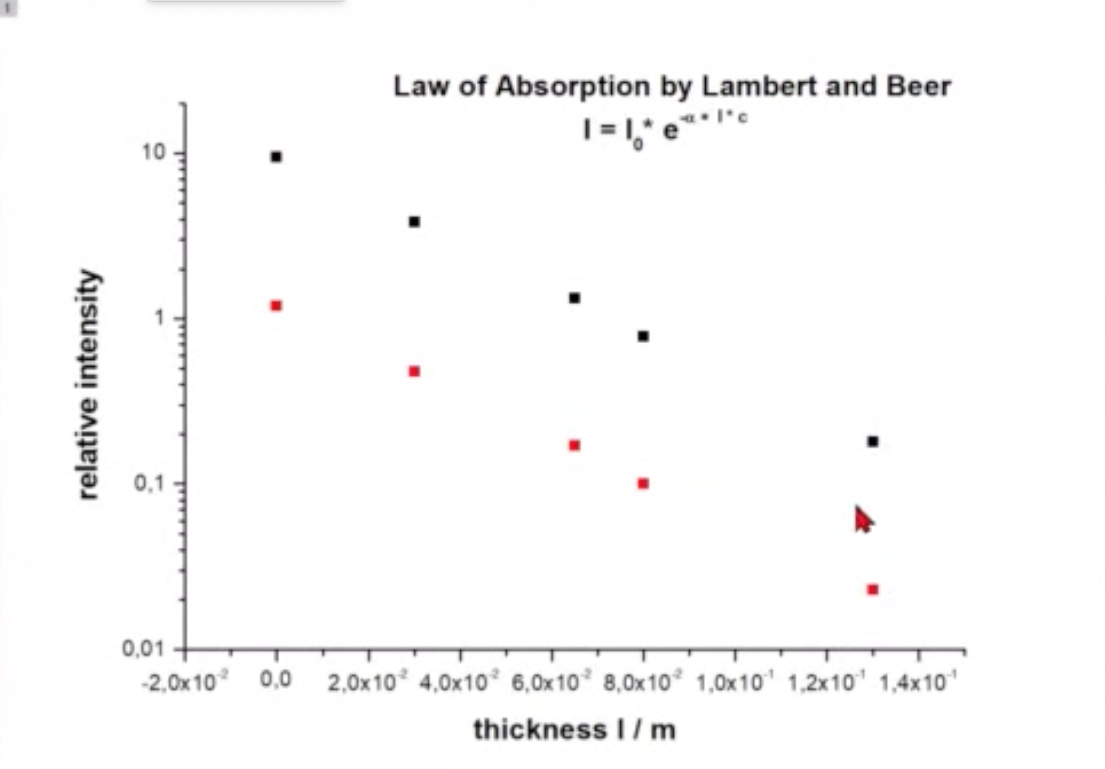
Fig.: .

As the coefficient \(\kappa\) shows the indicated frequency dependence, the absorption coefficient is also reflecting this strong absorption close to the resonances but weaker absorption far away from it. Since common materials have not only a single but many of hose resonances, the absorption behavior could be quite complex. It is however characteristic for each substance, which makes absorption spectroscopy a invaluable tool to study the composition of materials.

Dispersion

Besides the frequency dependence of the imaginary part of the refractive index, the real part has also a very pronanounced feature. This has consequences for the propagation speed of the wavefronts (phase velocity) or the speed of whole groups of waves, which is described by the group velocity \(v_g\).

We know already the definition of the phase velocity

\[v=\frac{\omega}{k} \tag{phase velocity}\]

The group velocity is given by

\[v_g=\frac{d\omega}{dk} \tag{group velocity}\]

The latter can be related to the refractive index \(n_r\) by

\[v_g=\frac{d}{dk}(v k)=v+k\frac{dv}{dk}\]

With the help of \(k=k_0 n_r\) and \(v=c/n_r\) this yields

\begin{eqnarray} v_g&=&v+k_0 n_r \frac{d}{dk}\left ( \frac{c}{n_r}\right)\\ &=&v-k_0 n_r c\frac{1}{n_r^2}\frac{dn_r}{dk} \end{eqnarray}

The derivative of the refractive index by the wavenumber can be obtained when looking at the total differebtial

\[dk=\frac{n_r}{c}d\omega+\frac{\omega}{c}d n_r\]

which gives

\[\frac{dk}{dn_r}=\frac{n_r}{c}\frac{d\omega}{d n_r}+\frac{\omega}{c}\]

The inverse of this expression can now be inserted in the group velocity and finally yields

\[v_g=\frac{c}{n_r+\omega \frac{dn_r}{d\omega}} \tag{group velocity dispersion}\]

Based on this equation, we may characterize the dispersion, i.e. the variation of the refractive index with the frequency. If the coefficient

\[\frac{dn_r}{d\omega}>0 \tag{normal dispersion}\]

is positive, we call this normal dispersion. This is what we observed for the refractive index when discussing the prism or the rainbow. The refractive index is larger for shorter wavelength then.

In the case when

\[\frac{dn_r}{d\omega}<0 \tag{anomalous dispersion}\]

we call this anomalous dispersion. In both cases we see the the change of the refractive index of materials with the frequency is related to the polarizability of the material and the specific resonances. Yetm our model has been very crude.

What we may also find is a situation when the group velocity is larger than the speed of light. For this to occur we need to have

\[n_r+\omega \frac{dn_r}{d\omega}<1\]

which is true for our susceptibility model at

\[|\omega_0-\omega|<\frac{\sigma}{2} \tag{$v_g>c$}\]

This might seem to contradict our assumption of having nothing which can move faster than the speed of light. However, this assumption is only valid for the transport of energy, matter or information, not for the group velocity.

The transport of energy given by

\[v_{E}=\frac{I}{w_{em}}\le c\]

is always smaller or equal to the speed of light.