This page was generated from `/home/lectures/exp3/source/notebooks/L4/Magnifying Glass.ipynb`_.

Magnifying Glass

A magnifying glass has several applications. First of all, it allows to see objects with details that would otherwise be too small to be observed with the eye even of the eye lens can accomodate to the distances. Such magnifying glasses are also used in microscopes as the so-called eye-piece as we will later see in the section on microscopes.

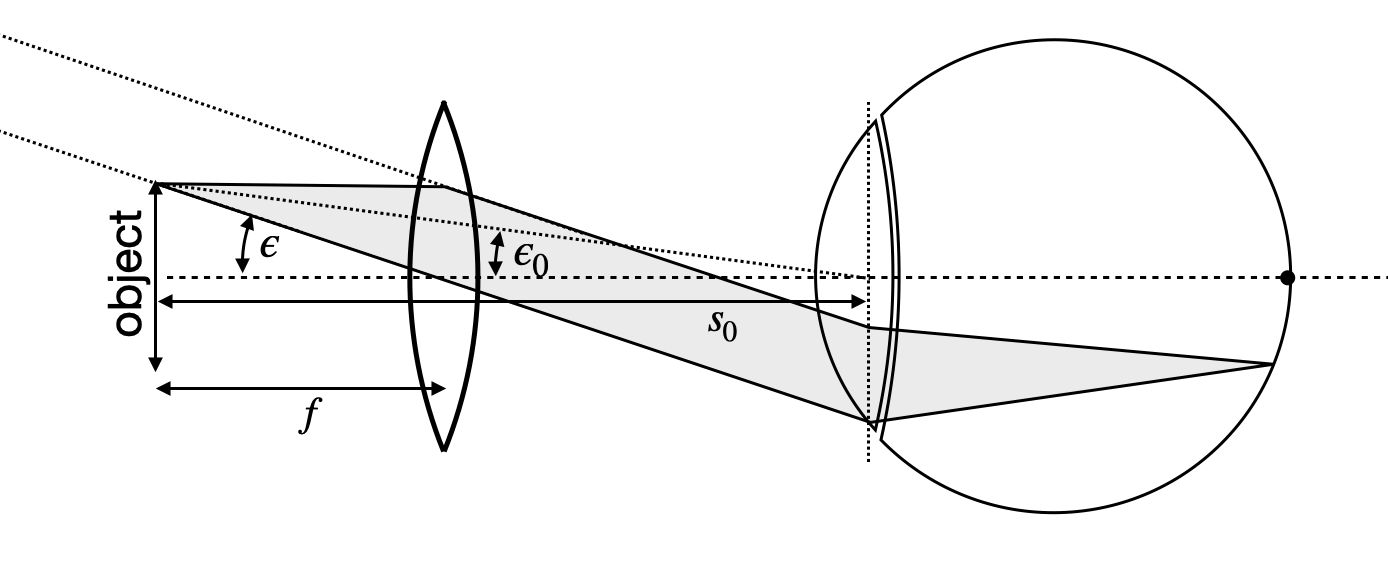
Consider the sketch below. The sketch shows an object of a size $A$ which is at a distance of $s_0$ from the eye. The object makes an angle ${ϵ}_0$ with the optical axis. If we insert now a lens into the space between object and eye and the lens is positioned in a way that it is exactly at a distance $f$ (the focal distance of the lens) from the object then we are able to observe the object under a different angle $ϵ$.

Fig.: Magnifying glass at the focal distance.

The magnification of this magnifying glass can the be calculated from the angles $ϵ\approx A/f$ and ${ϵ}_0\approx A/s_0$:

$$V=\frac{\tan (ϵ)}{\tan ({ϵ}_0)}\approx \frac{ϵ}{{ϵ}_0}=\frac{A}{f}\frac{s_0}{A}=\frac{s_0}{f}.$$

The angular magnification is, thus, just given by the ratio of the clear visual range to the focal distance of the lens. If the focal distance $f$ becomes much smaller than $s_0$, large magnifications are possible.

A second very useful effect is that when the object is placed inside the focal distance from the lens, the eye images a virtual image at infinite distance to the retina (see sketch). This means the eye muscle can stay relaxed when observing the object, while it would otherwise probably have to accommodate to the distance.

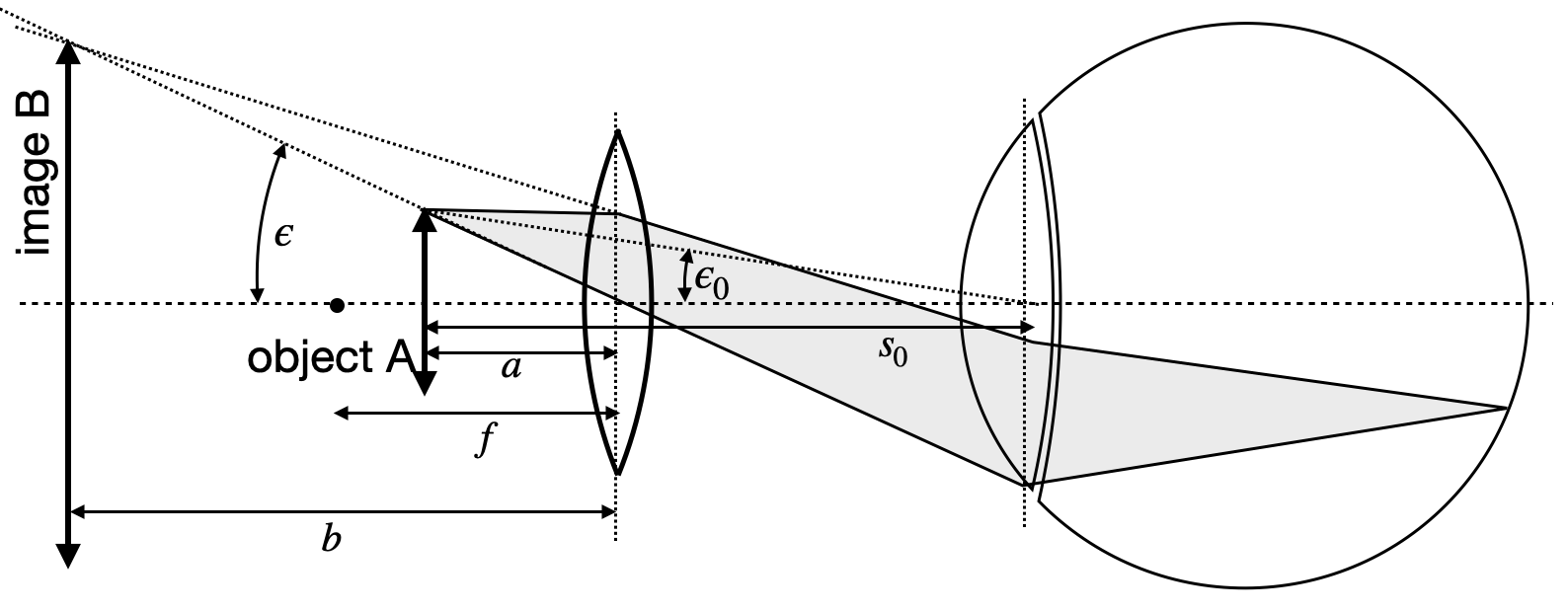
Yet, placing the object at exactly the focal distance is rather tedious when holding the magnifying glass by hand. If the object is now placed inside the focal distance of the magnifying glass, we may also calculate a magnification in this case knowing the virtual image size $B$ created in this case (see sketch below)

Fig.: Magnifying glass for an object inside the focal range of the lens.

If $a$ is the distance of the object from the principle plane of the magnifying glass and $b$ and $B$ are the distance and the size of the virtual image, respectively, we obtain

$$V=\frac{\tan (ϵ)}{\tan ({ϵ}_0)}\approx \frac{ϵ}{{ϵ}_0}=\frac{B}{b}\frac{s_0}{A}=\frac{s_0}{a}.$$

Using the imaging equation

$$\frac{1}{f}=\frac{1}{a}+\frac{1}{b}$$

we may finally arrive at

$$V=\frac{s_0(b-f)}{bf}$$

in this case. If we place the virtual image directly at the clear visual range, i.e., $b=-s_0$, we find

$$V=\frac{s_0}{f}+1.$$