This page was generated from `/home/lectures/exp3/source/notebooks/L12/Diffraction Grating.ipynb`_.

Diffraction Grating

Spectral resolution

For the spectral resolution we have to define a criterium again, that allows us to quantify the spectral resolution. We borrow the idea we used from the optical resolution of the microscope, i.e. that two peaks are separable, if the second peak is located at the minimum of the first diffraction pattern. Here the diffraction patterns refer not to different objects on space but to different wavelength ${\lambda }_1$ and ${\lambda }_2$.

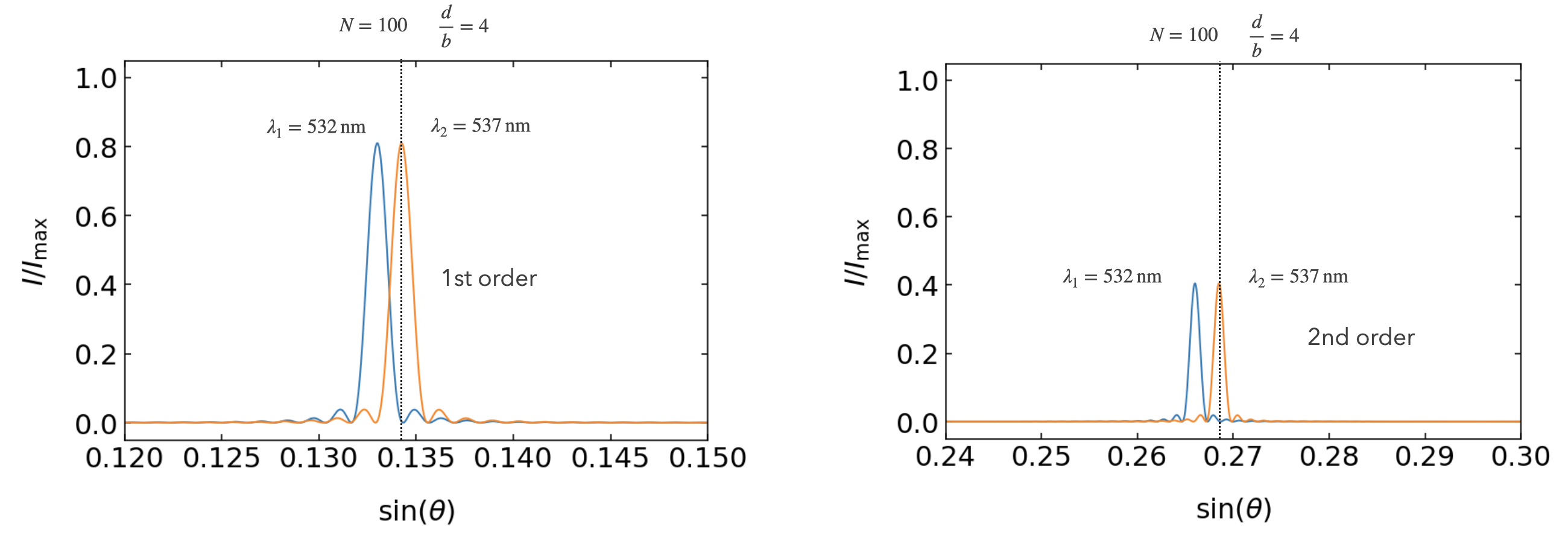
Fig.: Rayleigh resolution limit a grating with $N=100$ slits ($d=4$ µm, $b=1$ µm) with ${\lambda }_1=532$ nm and ${\lambda }_2=537$ nm in the first order diffraction peak (left) and the second order peak (right).

Let us have a look at the $m$th order diffraction peak for the wavelength ${\lambda }_1$. This occurs at

$$\sin (\theta )=m\frac{{\lambda }_1}{d}$$

The next secondary minimum to larger angles of the diffraction pattern is then located at a position, where the numerator of the multiple wave interference

$${\sin }^2(N\pi \frac{d}{\lambda }\sin (\theta ))$$

becomes zero or the argument

$$N\pi \frac{d}{\lambda }\sin (\theta )=l\pi$$

becomes a multiple $l$ of $\pi$. For the first order main peak we have had already $N-2$ intermediate peaks as well as the 0th and now the first order peak. Therefore $m=l/N$ and the next mimimum after the 1st order peak is at

$$\sin ({\theta }_1)=\frac{l+1}{N}\frac{{\lambda }_1}{d}$$

This angle has to correspond to the position of the main peak of the first order diffraction of the wavelength ${\lambda }_2$, so

$$\sin ({\theta }_1)=m\frac{{\lambda }_2}{d}$$

Combining both equations for the two wavelength yields

$$(m+\frac{1}{N})\frac{{\lambda }_1}{d}=m\frac{{\lambda }_2}{d}$$

and after some rearrangements (and setting \lambda_1=:nbsphinx-math:lambda)

$$R=\frac{\lambda }{\mathrm{\Delta }\lambda }=mN$$

This is the resolving power $R$ of a grating. The ability to resolve two wavelength therefore increases with the diffraction order $m$ and the number of slits used for the diffraction. Yet, the intensity of higher diffraction orders rapidly decreases due to the grating envelope. Therefore, the main parameter to change is the number of illuminted slits.

Our finding is illustrated in the Figure above. Where we achieve a resolution of about 5 nm, when using $N=100$ slits at a distance of $d=4$ µm.

Fig.: Diffraction pattern observed for a grating in the lecture with red light (left) and white light (right).