This page was generated from `/home/lectures/exp3/source/notebooks/L9/MultiWave Interference.ipynb`_.

Multiple Wave Interference

So far we looked at the interference of two waves, which was a simplification as I mentioned already earlier. Commonly there will be a multitude of partial waves contribute to the oberved intereference. This is what we would like to have a look at now. We will do that in a quite general fashion, as the resulting formulas will appear several times again for different problems.

Nevertheless we will make a difference between

• multiwave interference of waves with the same amplitude

• multiwave interference of waves with decreasing amplitude

Especially the latter is often occuring, if we have multiple reflections and each reflection is only a fraction of the incident amplitude.

Multiple Wave Interference with Constant Amplitude

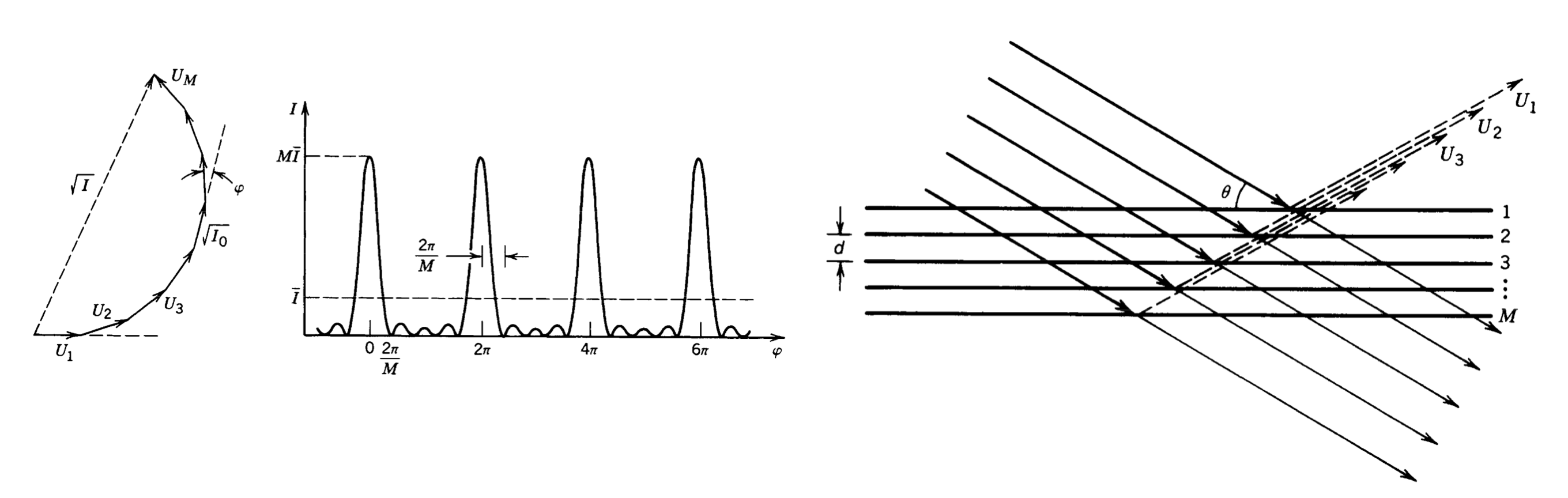
In the case of constant amplitude (for example realized by a grating, which we talk about later), the total wave amplitude is given according to the picture below by

\[U=U_1+U_2+U_1+U_3+\ldots+U_M\]

where we sum the amplitude over \(M\) partial waves. Between the neighboring waves (e.g. \(U_1\) and \(U_2\)), we will assume a phase difference (because of a path length difference for example), which we denote as \(\phi\).

The amplitude of the p-th wave is then given by

\[U_p=\sqrt{I_0}e^{i(p-1)\phi}\]

with the index \(p\) being an interger \(p=1,2,\ldots,M\), \(h=e^{i\phi}\) and \(\sqrt{I_0}\) as the amplitude of each individual wave. The total amplitude \(U\) can be then expressed as

\[U=\sqrt{I_0}\left (1+h+h^2+\ldots +h^{M-1}\right)\]

which is a geometric sum. We can apply the sum formula for geometric sums to obtain

\[U=\sqrt{I_0}\frac{1-h^M}{1-h}=\sqrt{I_0}\frac{1-e^{iM\phi}}{1-e^{i\phi}}\]

We now have to calculate the intensity of the total amplitude

\[I=|U|^2=I_{0}\left | \frac{e^{-iM\phi/2}-e^{iM\phi/2}}{e^{-i\phi/2}-e^{i\phi/2}}\right |^2\]

which we can further simplify to give

\[I=I_{0}\frac{\sin^2(M\phi/2)}{\sin^2(\phi/2)}\]

Fig.: Multiple wave interefence. Left: Phase construction of a multiwave intereference with M equal amplitude waves. Middle: Intensity distribution obtained as a function of the phase shift \(\phi\). Right: Examplary sketch of the interference generation.

The result is therefore an oscillating function. The numerator \(\sin^2(M\phi/2)\) shows and oscillation frequency, which is by a factor of \(M\) higher than the one in the denominator \(\sin^2\phi/2)\). Special situations occur, whenever the numerator and the denominator become zero. This will happen whenever

\[\phi=m 2\pi\]

where \(m\) is an integer and denotes the interference order, i.e. the number of wavelength that neighboring partial waves have as path length difference. In this case, the intensity distributiion will give us

\[I=I_0 \frac{0}{0}\]

and we have to determine the limit with the help of l’Hospitals rule. The outcome of this calculation is, that

\[I(\phi=m2\pi)=M^2 I_0\]

which can be also realized when using the small angle approximation for the sine functions.

Since he numerator is much faster oscillating then the denominator, we may also encounter the situation, where the numerator is zero, but the denomintor is not. These situations result in the additional minima between the primary maxima. We will have exactly \(M-1\) minima between the global maxima and \(M-2\) primary maxima. We will come back to these details when we talk about the diffraction grating in the next section.

Multiple Wave Interference with Decreasing Amplitude

We will turn our attention now to a slight modification of the previous multiwave interference. We will introduce a decreasing amplitude of the individual waves. The first wave shall have an amplitude \(U_1=\sqrt{I_0}\). The next wave, however, will not only be phase shifted but also have a smaller amplitude.

\[U_2=h U_1\]

where \(h=re^{i\phi}\) with \(|h|=r<1\). \(r\) can be regarded as a reflection coefficient, which deminishes the amplitude of the incident wave. According to that the intensity is reduced by

\[I_2=|U_2|^2=|h U_1|^2=r^2 I_1\]

The intensity of the incident wave is multiplied by a factor \(r^2\), while the amplitude is multiplied by \(r\). Note that the phase factor \(e^{i\phi}\) is removed when taking the square of this complex number.

Intensity at Boundaries

The amplitude of the reflected wave is diminished by a factor \(r\le 1\), which is called the reflection coefficient. The intensity is diminished by a factor \(R=|r|^2\le1\), which is the reflectance.

In the absence of absorption, reflectance \(R\) and transmittance \(T\) add to one due to energy conservation.

\[R+T=1\]

Consequently, the third wave would be now \(U_3=hU_2=h^2U_1\). The total amplitude is thus

\[U=U_1+U_2+U_3+\ldots+U_M = \sqrt{I_0}(1+h+h^2+\ldots)\]

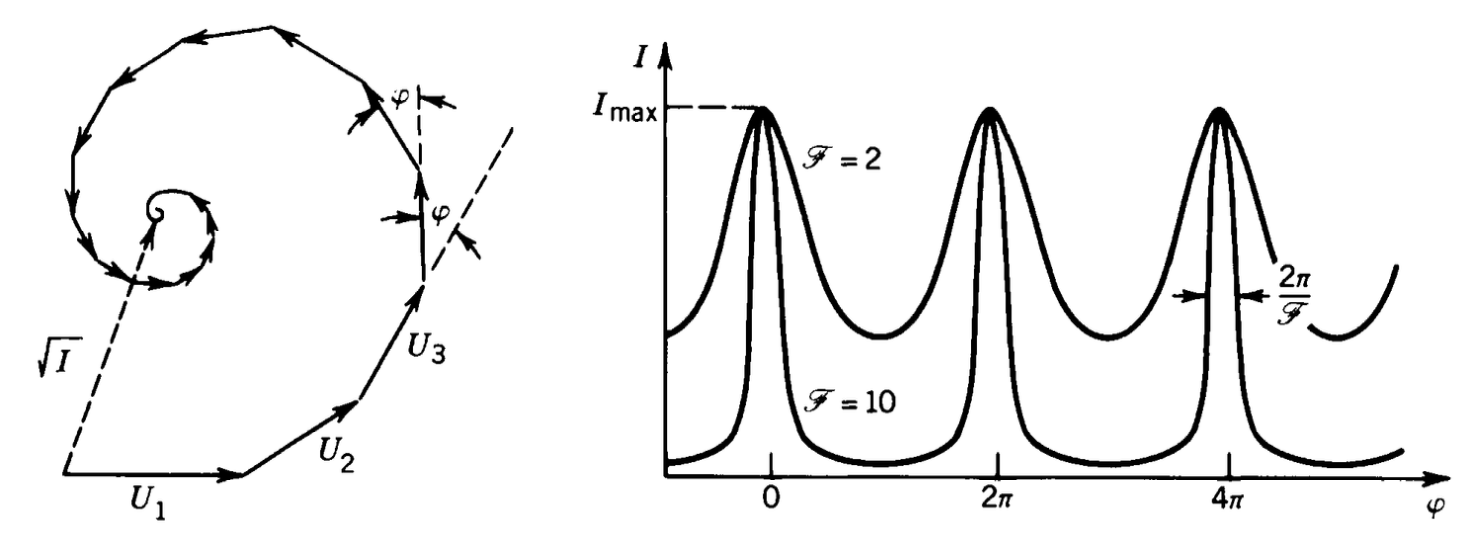
Fig.: Multiple wave interefence with decreasing amplitudes. Left: Phase construction of a multiwave intereference with M equal amplitude waves. Right: Intensity distribution obtained as a function of the phase shift \(\phi\).

This yields again

\[U=\sqrt{I_0}\frac{(1-h^M)}{1-h}=\frac{\sqrt{I_0}}{1-r e^{i\phi}}\]

Calculating the intensity of the waves is giving

\[I=|U|^2=\frac{I_{0}}{|1-re^{i\phi}|^2}=\frac{I_0}{(1-r)^2+4r\sin^2(\phi/2)}\]

which is also known as the Airy function. This function can be further simplified by the following abbrevations

\[I_{\rm max}=\frac{I_0}{(1-r)^2}\]

and

\[\mathcal{F}=\frac{\pi \sqrt{r}}{1-r}\]

where the latter is called the Finesse. With those abbrevations, we obtain

\[I=\frac{I_{\rm max}}{1+4\left(\frac{\mathcal{F}}{\pi}\right)\sin^{2}(\phi/2)}\]

for the interference of multiple waves with decreasing amplitude.

This intensity distribution has a different shape than the one we obtained for multiple waves with the same amplitude.

Fig.: Multiple wave interference with decreasing amplitude. The graph shows the intensity distribution over the phase angle \(\phi\) for different values of the Finesse \(\mathcal{F}\).

We clearly observe that with increasing Finesse the intensity maxima, which occur at multiples fo \(\pi\) get much narrower. In addition the regions between the maxima show better contrast and fopr higher Finesse we get complete destructive interference.