This page was generated from `/home/lectures/exp3/source/notebooks/L12/Fresnel Zones.ipynb`_.

Fresnel Zones

We want to have a more general look at diffracion and just take a detour over a concept, which is called Fresnel zones. We have a look at spherical waves of a wavelength $\lambda$ which are emitted from a source as indicated by the solid line in the sketch below.

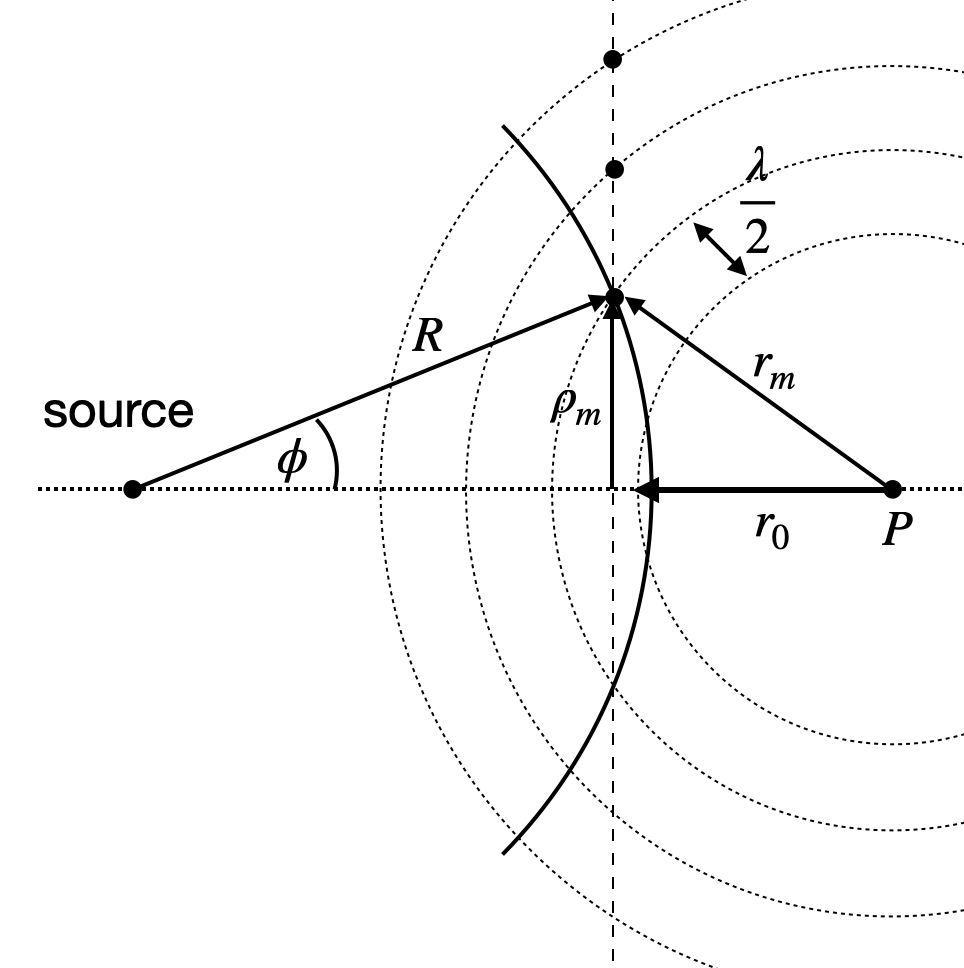
Fig.: Construction of the Fresenel Zones.

We will have a look at the intensity of the wave at a point $P$. For that purpose we look at the amplitude from all points of the wavefront, as on the wavefront, there are Huygens sources, which contribute to the intensity at point $P$.

We will not calculate the intensity explicitly, but rather analyze the distance of the individual points on the wavefront from the point $P$. In particular, we may have a look at look at concentric circles around the point $P$, where the radius of the circles grows by $\lambda /2$, i.e.

$$r_m=r_0+m\frac{\lambda }{2}$$

where $m$ is an integer. These regions between $r_m$ and $r_{m+1}$ are called Fresnel zones. If we consider now two neighboring zones, then there is in each zone a pair of points, which are exactly $\lambda /2$ out of phase. This means that those two contibutions would lead to destructive interference. If we remove those points, we will be left with constructive interference on the axis only. We can construct such an aperture, if we calculate the ring radius

$${\rho }_m^2={(r_0+m\frac{\lambda }{2})}^2-r_0^2$$

according to the sketch above. This yields

$${\rho }_m^2=r_{0}m\lambda +m^2\frac{{\lambda }^2}{4}$$

For $r_0\gg \lambda$ we can simplify the above formula to

$${\rho }_m=\sqrt{m{r}_0\lambda }$$

which gives the radius of the individual zones. The width of the zones is given by

$$\mathrm{\Delta }{\rho }_m={\rho }_{m+1}-{\rho }_m=\sqrt{r_0\lambda }(\sqrt{m+1}-\sqrt{m})$$

Fresnel Zone Plate

If we now fill on a glass slide the ring ${\rho }_m$ to ${\rho }_{m+1}$ but leave ${\rho }_{m+1}$ to ${\rho }_{m+2}$ transparent we create a so called Fresnel zone plate. Here the radius in the first zone $r$ ranges from $r_0$ to $r_0+\lambda /2$. The next zone will range from $r_0+\lambda /2$ to $r_0+\lambda$ but is removed from its contribution to the point.

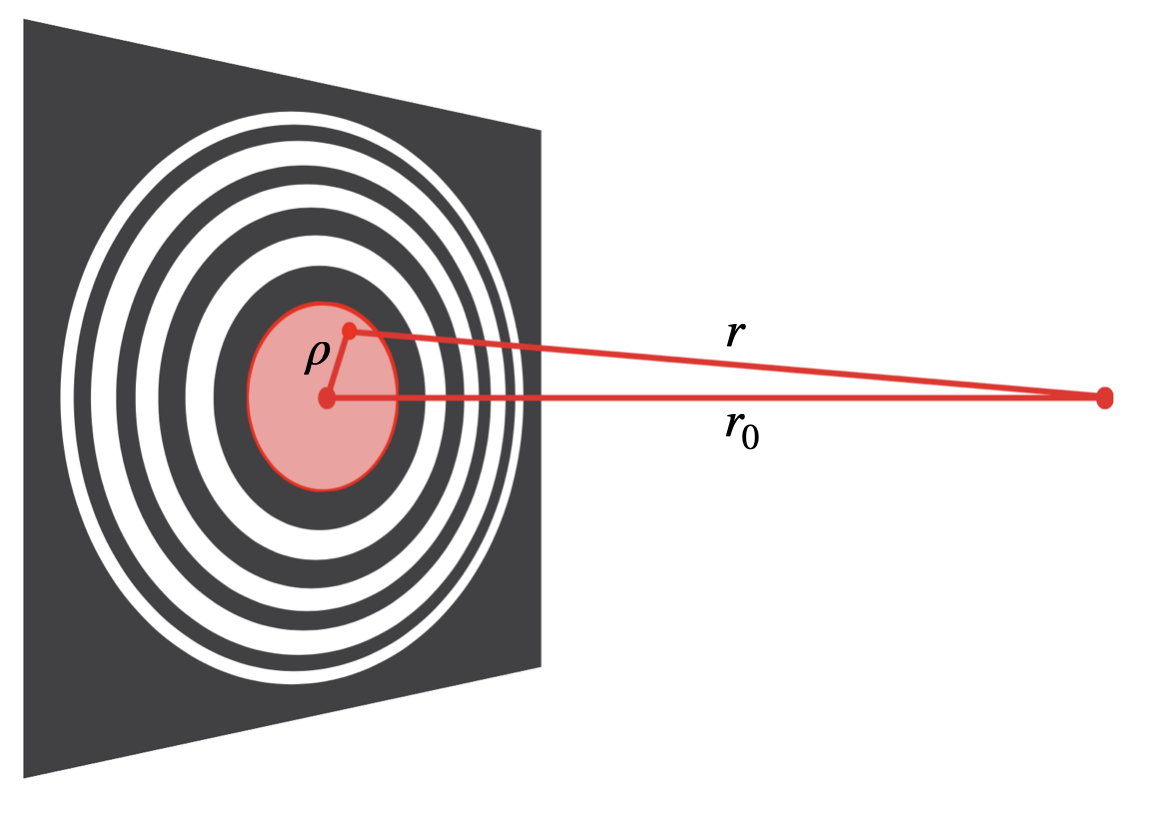
Fig.: Fresnel zone plate removing destructive interference to the point on the optical axis.

The Fresnel zones plate may be constructed by defining the inner reference zone in an arbitrary way. One may either block or transmit the direct path from the light source along the optical axis and thus have either the odd or even zones transparent.

Fig.: Fresnel zone plates with odd (left) or even (right) zones transparent delivering the same result.

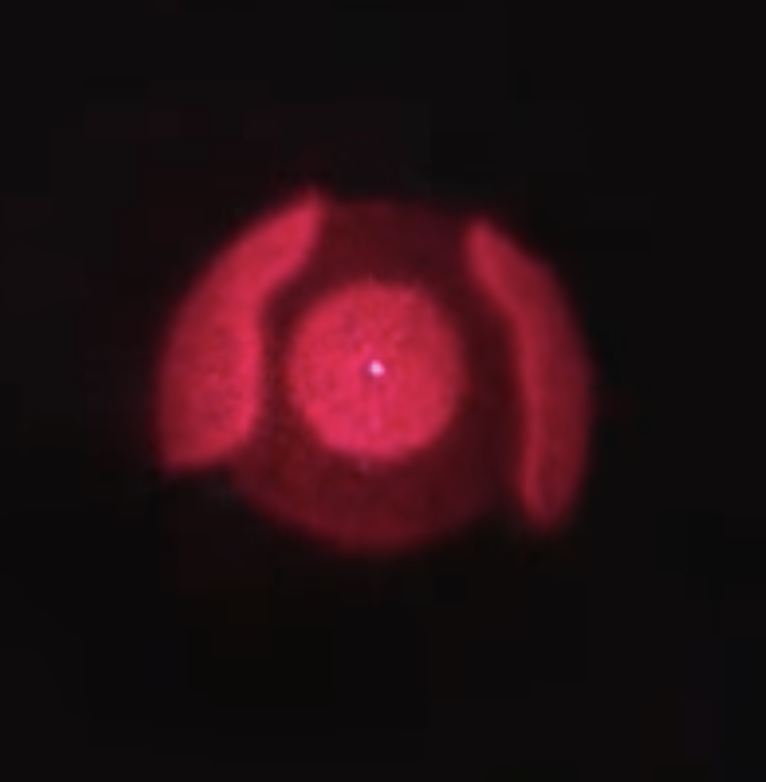
Fig.: Fresnel zone plate used in the lecture (left), which actually cracked due to the heat of the light source a second later. The Fresnel zone plate creates a focal point as visbile on the right (bright spot in the center).

Such zone plates are important for applications, when for example the focusing of radiation has to be achieved but refractive indices are not large enough to create a strong enougth refraction. This is especially true for X-ray radiation.

Fig.: Fresnel zone plates for X-ray radiation. Image taken from Ion beam lithography for Fresnel zone plates in X-ray microscopy - Optics Express, Vol. 21 Issue 10, pp.11747-11756 (2013).