This page was generated from `/home/lectures/exp3/source/notebooks/L4/Optical Instruments.ipynb`_.

Optical Instruments

Optical instruments now combine a number of optical elements or even consist only out of a single one as in the case of the magnifying glass or the eye.

The Eye

The human eye is certainly one of the most amazing biological sensorial systems, which consists of biologically grown optical elements including an aperture, an adaptive lens and a photodetector, which is connected to an intelligent neural network, that is amazingly accurate and fast in pattern recognition. Think of that for a moment, that this performance is given with a few 10 W power consumption and then turn around your laptop and check out its power consumption.

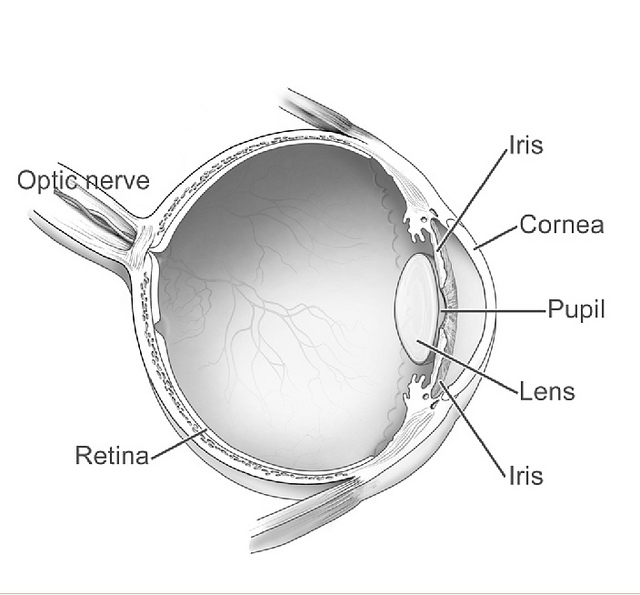
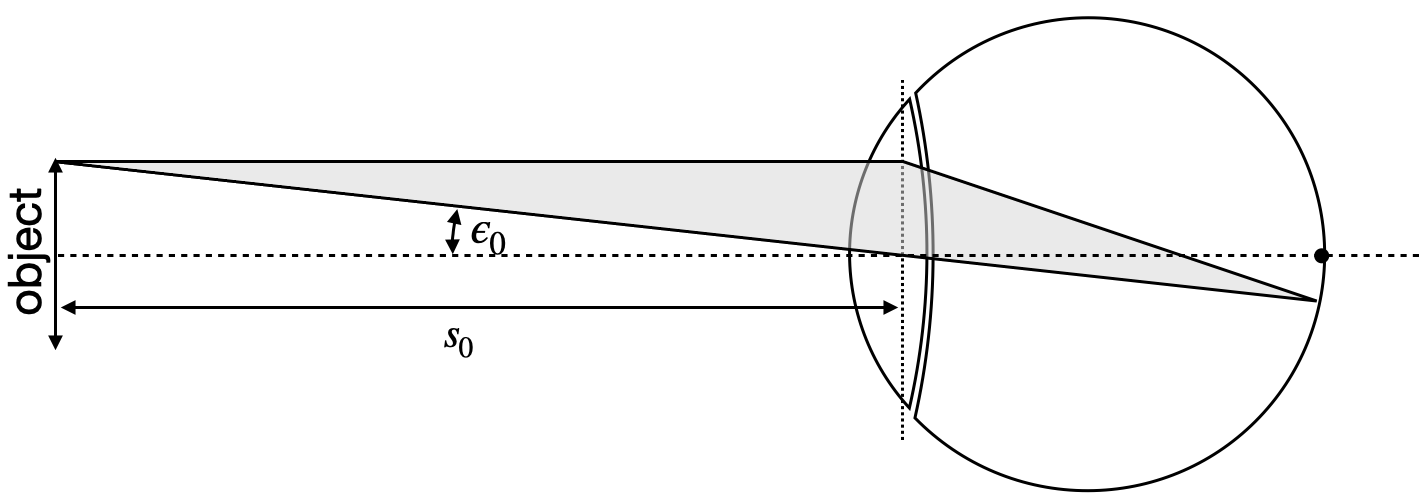
The eye allows you to image objects at variable distance from you. The sketch below indicates some of its essential ingredients.

Fig.: Sketch of the ingredients of the human eye. Most important parts the lens, the glass body and the retina containing the bightness (rods) and color sensors (cones). A more detailed sketch is depicted on the right side, which shows the arrangement of rods and cones in the retina including their parallel connection. Their combined signal is ending the optical nerves guiding the signals to the brain.

Most important is the pupil resembling an adjustable aperture for adjusting the total light falling to the retina and the lens, connected to muscles to change the curvature of the lens and, thus, also the focal distance.

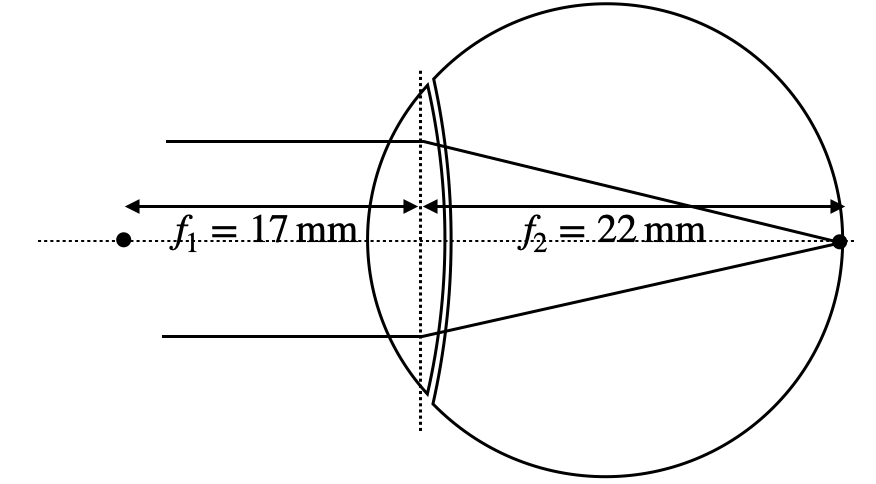
The lens is connected to air on one side as the surrounding medium and to a vitreous humor (glass body) on the other side. So there is some asymmetry. The eye, therefore, has a front focal length of \(f_1=17\,{\rm mm}\) and a back focal length of \(f_2=22\,{\rm mm}\). These values may vary by the individual but also by the distance of the object. For close objects the eye can accomodate its focal distance to \(f_1=14\,{\rm mm}\) and \(f_2=19\,{\rm mm}\).

Fig.: Focal distances for the eye lens.

Cones and rods are differently distributed around the fovea, which is the spot of the highest color sensitivity. The cone density peaks around this center, while the rod density is larger outside. Cones are the color sensitive objects, which gain their light sensitive from a dye molecules called retinal undergoing a conformational transition upon excitation with light. This triggers a cascasde of different chemical processes. Cones with three narrow excitation ranges allow our color vision (see Fig. below).

Fig.: Angular distribution of cones and rods around the fovea, electron micrograph of cones (large) and rods (small) as well as their color sensitivity.

Under normal conditions, objects at infinite distance are imaged to the retina at the back focal distance \(f_2=22\, {\rm mm}\). However, the lens of the eye may have defects changing its refractive power. Often this leads to short-sightedness or far-sightedness. If you are short-sighted, the light from infinite distance is not focused to the retina but to some shorter distance inside the glass body. This may be corrected by a concave lens as displayed in the image below on the left side. If you are far-sighted, then the light is focused behind the retina if objects are ininitely distant away. To correct for that error, one needs a convex lens as displayed on the right side.

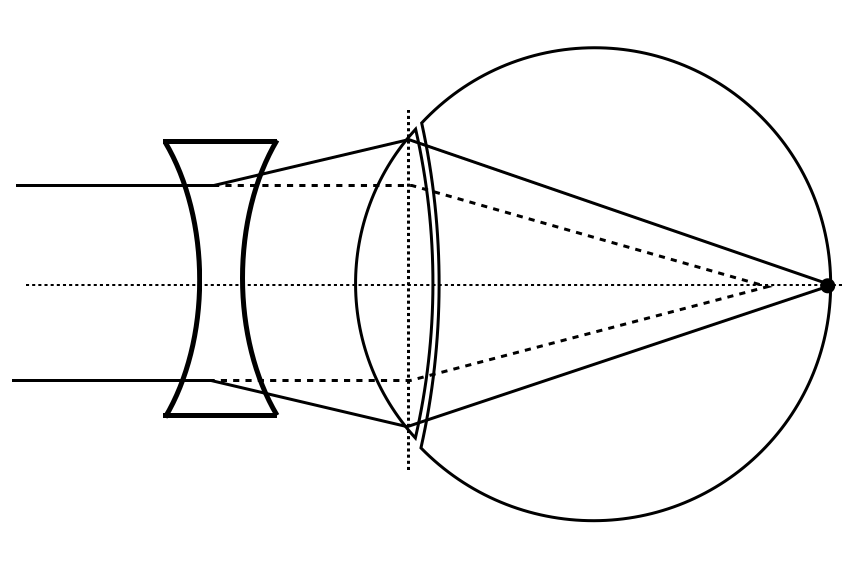
Fig.: Short-sightedness (left) and far-sightedness (right) and their correction by additional lenses.

In the normal relaxed state of the eye muscle, one can, therefore, observe objects up to a distance of \(s_0=25\, {\rm cm}\) without additional accomodation of the eye lens. This distance, which varies from person to person, is standardized and called the range of clear visual sight. This range of clear visual sight allows to observe objects under an angle \(\epsilon\).

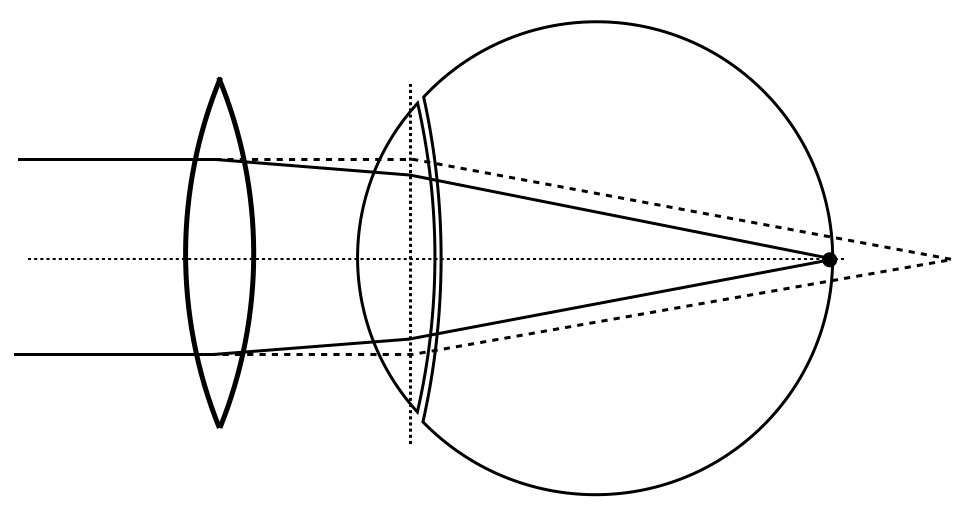
Fig.: Short-sightedness (left) and far-sightedness (right) and their correction by additional lenses.

Instead of calculating the magnification of the following optical instruments from the object and image distances, we refer now to a different measure, which is the angular magnification. The angular magnification is given by

\[V=\frac{\tan(\epsilon)}{\tan(\epsilon_0)}\approx \frac{\epsilon}{\epsilon_0}.\]

This is a useful measure as the image size is not really accessible ;-).