This page was generated from `/home/lectures/exp3/source/notebooks/L18_AMA/Metals.ipynb`_.

Metals

Metals have free charges, which modify the propagation of light. Their influence is large and gives metals their characteristic reflection and color. In this case, we have to include the free charge density \(\rho_f\) and the current density \(\vec{j}\) in the Maxwell equations and derive the wave equation accordingly. Instead of modifying the wave equation, we would like to go a different way here. We would like to derive the dielectric function for metals based on a microscopic description, which is only approximate but captures some basic features.

Drude Model

The model we would like to put forward is the Drude model. It considers the motion of a charge in the electromagnetic field of a wave. As compared to our previous attempts on bound electrons in atoms, there is no direct restoring force for the free charges in the metal. The equation of motion therefore looks as

\[m_e\frac{d^2\vec{r}}{dt^2}+m_e\Gamma \frac{d\vec{r}}{dt}=e\vec{E}_0 e^{i\omega t}\]

Here, the coefficient \(\Gamma\) is given by

\[\Gamma=\frac{v_f}{l}=\frac{1}{\tau}\]

where \(v_f\) is the so-called Fermi energy and \(l\) is the mean free path electrons travel before colliding with a lattice site inside the metal. To obtain an expression for the refractive index, we use again the ansatz

\[\vec{r}=\vec{r}_0 e^{i\omega t}\]

from which we obtain an expression for \(\vec{r}_0\). With his solution we can again calculate the polarization density and finally also the dielectric function

\[\epsilon_r(\omega)=n^2=1-\frac{\omega_p^2}{\omega^2-i\Gamma \omega}\]

with

\[\omega_p=\sqrt{\frac{Ne^2}{\epsilon_0 m}}\]

which is called the plasma frequency. It is a characteristic for each metal, since the density of free charges in the metal enters the equation. It is located in the UV region of the electromagnetic spectrum.

Dielectric function

With our previous definition of the complex refractive index we may now analyze the result of the dielectric function in terms of the Drude model. Using

\[n=n_r-i\kappa\]

the dielectric function, which is the square of the refractive index, is given by

\[n^2=n_r^2-\kappa^2-2i n_r \kappa=\epsilon^{\prime}+i\epsilon^{\prime\prime}\]

We can therefore relatex the real part

\[\epsilon^{\prime}=n_r^2-\kappa^2=1-\frac{\tau^2 (\omega^2-\omega_p^2)}{1+\omega^2\tau^2}\]

and the imaginary part

\[\epsilon^{\prime\prime}=2n_r\kappa=\frac{\omega_p^2\tau}{\omega(1+\omega^2\tau^2)}\]

of the dielectric function \(\epsilon=\epsilon^{\prime}+i\epsilon^{\prime\prime}\) to the refractive index components.

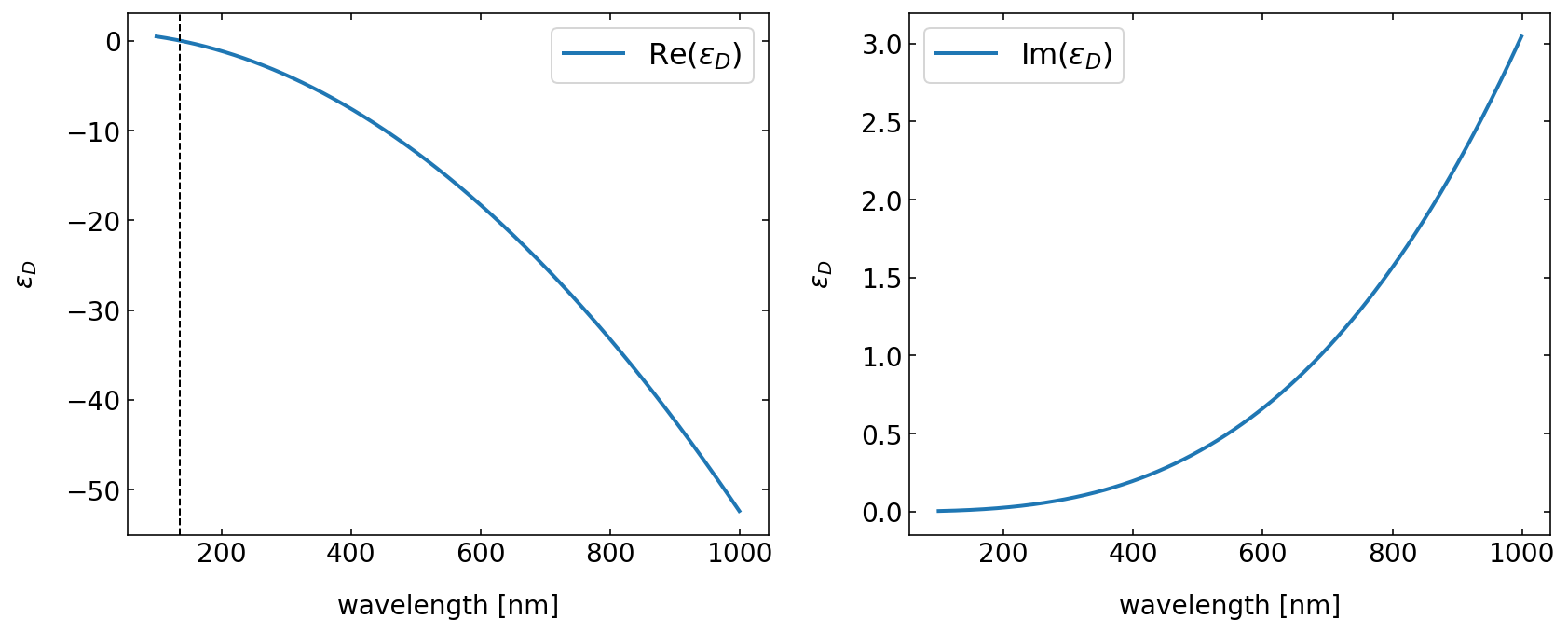
Fig.: Real (left) and imaginary part (right) of the dielectric function according to the Drude model. The dashed line in the left plot corresponds to the plasma frequency. The calculations are for Gold.

The figure above shows the dielectric function for Gold as determined from the parameters \(\omega_{p}=13.8\times 10^{15}\, \rm{s}^{-1}\) and \(\Gamma=1.075\times 10^{14}\, \rm{s}^{-1}\). The real value of the dielectric function is negative over the whole visible range stating that there is no propagating wave inside the matal. It just becomes positive below the plasma frequency. The imaginary part increases continuously with the wavelength.

Conductivity

As we calculate the position \(\vec{r}\) of the electrons in the oscillating electric field, we may also obtain its velocity. This helps us to calculate a new quantity, which is the conductivity \(\sigma\) of the metal. This conductivity will be frequency dependent as well as the charges will not follow the electric field oscillations in the same way at different frequencies. The conductivity is following from Ohm’s law, which is given by

\[\vec{j}=\sigma \vec{E}=N e \vec{v}\]

where we explicity wrote the current density on the right side. Following this relation, the conductivity is obtained as

\[\sigma=\epsilon_0 \omega_p^2\frac{\tau(1+i\omega\tau)}{1+\omega^2\tau^2}\]

from the Drude model and we may express the real and imaginary parts of the dielectric function also in relation to the conductivity by

\[\epsilon^{\prime}=1-\frac{\mathcal{R}(\sigma)\tau}{\epsilon_0}\]

\[\epsilon^{\prime\prime}=\frac{\mathcal{Im}(\sigma)}{\epsilon_0 \omega^2 \tau}\]

which readily tells us, that we obtain information about conductivity at high frequencies from optical measurements.

Fig.: Backscattering and transmission through a 65 nm gold nanoparticle solution. The backscattering is green due to the surface plasmon resonance of the conduction band electrons, while the transission is red, since the green light is removed by scattering.